WASMOD
Ein Modellsystem zur gebietsbezogenen Simulation von Wasser- und Stoffflüssen
Darstellung des aktuellen Entwicklungsstandes
ECOSYS 1996
Ernst-Walter Reiche, Projektzentrum Ökosystemforschung Kiel
Text Download (Ami Pro Dokument als WinZip-File)
Abstract
Das Modellsystem WASMOD (Water and Substance Simulation Model) bietet die Möglichkeit, die Wasser- und Stoffdynamik von Gewässereinzugsgebieten zu berechnen. Durch Koppelung an ein Geographisches Informationssystem mittels geeigneter Parameterisierungsprogramme können Simulationsrechnungen in hoher räumlicher und zeitlicher Auflösung durchgeführt werden. Neben der Beschreibung der Systemkonzeption sowie der wichtigsten Teilmodelle wird ein Überblick über die bisher durchgeführten Modellanwendungen geliefert.
Einführung
Im Rahmen des Forschungsvorhabens "Ökosystemforschung im Bereich der Bornhöveder Seenkette" stellt die Erfassung von Wasser- und Stoffflüssen - innerhalb und zwischen Ökosystemen - einen wichtigen Arbeitsschwerpunkt dar. Ein umfangreiches Meßprogramm liefert Daten zur Bilanzierung der N-Einträge in die einzelnen Systemkompartimente sowie zur Quantifizierung der für den Haushalt wichtigen Transport- und Transformationsprozesse (SCHIMMING et al. 1995, HÖRMANN et al. 1992, SPRANGER 1992). Diese Untersuchungen werden in terrestrischen (Acker, Grünland, Wälder), semiterrestrischen (Feuchtgrünland, Erlenbruch, Niedermoorgebiete) und in limnischen Ökosystemen durchgeführt. Ziel ist es u.a., vom lokalen bis zum regionalen Maßstab die Wirkungsweise und die Effektivität der miteinander vernetzten Prozesse aufzuzeigen und den Einfluß unterschiedlicher menschlicher Eingriffe abzuschätzen. Die mittel- und langfristige Wirkung von anthropogen bedingten Stoffeinträgen in Ökosysteme unterschiedlicher Empfindlichkeit ist hierbei ein wichtiger Aspekt. Da nicht alle relevanten Prozesse durch Messungen erfaßt werden können, bzw. der Meßaufwand für viele Prozeßbeobachtungen zu hoch und zu kostenträchtig ist, stellt die Entwicklung und Anwendung von Simulationsmodellen einen wichtigen Teilbereich der Arbeiten dar. Ausreichend validierte Modelle bieten die Möglichkeit, Prozesse im Rahmen eines festzulegenden Gültigkeitsbereiches zeitlich und räumlich zu extrapolieren. Sie können beispielweise zur Durchführung regionaler Sensitivitätsstudien bzw. zur Abschätzung von langfristigen Entwicklungstendenzen und Gefährdungspotentialen eingesetzt werden. Darüber hinaus lassen sie sich als Hilfsmittel bei der Überprüfung und Weiterentwicklung theoriebezogener Aussagen zum Verhalten von Ökosystemen verwenden.
Das Modellsystem WASMOD (Water and Substance Simulation Model; REICHE 1991, 1994) ist modular aufgebaut und bietet die Möglichkeit, Simulationsrechnungen zur Wasser- und Stoffdynamik sowohl bezogen auf Einzelstandorte als auch im regionalen Maßstab für ganze Einzugsgebiete durchzuführen. In Abhängigkeit von den jeweils unterschiedlichen Raumausschnitten zugeordneten Parametern zur Kennzeichnung der Vegetation, der Relief- und Bodencharakteristika sowie agrartechnischer Nutzungsmaßnahmen erfolgt die Prozeßbeschreibung auf unterschiedlichen, hierarchisch angeordneten Raumeinheiten. Die Beschreibung der unterschiedlichen Transport- und Transformationsprozesse bezieht sich auf die Vegetationsschicht, auf die Bodenoberfläche, auf den durchwurzelten Boden sowie auf die ungesättigte und gesättigte Zone. Die Simulation der Transportprozesse erfolgt 'quasi-3-dimensional', d.h. vertikale und laterale Transportprozesse werden pro Zeitschritt nacheinander simuliert. Lateraler Transport findet in der Simulation nur an der Bodenoberfläche und im Grundwasserleiter statt, eine vergleichsweise einfache Lösung zur Simulation lateraler Wasserbewegung als Interflow wird zur Zeit getestet.
Im Vergleich mit anderen Entwicklungen füllt das Modellsystem eine wichtige Lücke zwischen Modellen, deren Schwerpunkt in der Beschreibung von pflanzenphysiologischen Prozessen liegt und die insbesondere die standortbezogene Prognose des Biomassenzuwachses anstreben (HOFFMANN 1995, BOSSEL und SCHÄFER 1989) und solchen, die die bodenchemischen und physikochemischen Prozesse unter 'steady state' Bedingungen beschreiben (z.B. WARFVINGE et al. 1992, REUSS and JOHNSON 1986) bzw. nur punktbezogen Simulationsrechnungen zur Wasser- und Stoffdynamik von Einzelstandorten liefern. Gerade die Möglichkeit, mit dem Modellsystem WASMOD gebietsübergreifend Wasser- und Stoffbilanzen bei flächenscharfer Detailauflösung rechnen zu können, macht eine Anwendung im Rahmen von Planungsverfahren besonders interessant. Eine besondere Beachtung finden die von Mikroorganismen gesteuerten Umsetzungsprozesse und ihre spezifischen Abhängigkeiten zum Kohlenstoff- und Stickstoffhaushalt. Bei der Entwicklung dieser Teilmodule konnte auf Prozeßbeschreibungen aus sogenannten Agrarökosystemmodellen zurückgegriffen werden (JONES and KINREY 1986, HANSEN et al. 1990). Ein wichtiges Anliegen bei der Formulierung einzelner Teilmodelle war die Beschränkung auf wenige, möglichst allgemein und flächendeckend verfügbare Eingangsparameter bei ausreichender Aussagegenauigkeit. Anhand von durchgeführten Untersuchungen zum Wasser- und Stickstoffhaushalt unterschiedlich genutzter Standorte wurde die Validität der einzelnen Modellteile überprüft. Um einen flächenhaften Modelleinsatz zu ermöglichen, wurden Verfahren zur Ableitung von Modellparametern entwickelt, die in Verbindung mit einem "Geographischen Informationssystem" (ARC/INFO) und einem Datenbanksystem größere Gebietssimulationen zulassen.
Im Rahmen dieses Beitrages kann keine ausführliche Beschreibung im Sinne einer Modelldokumentation geliefert werden, da das Modellsystem mitsamt der dazu entwickelten Parameterisierungsverfahren einen solchen Umfang erreicht hat, daß ein separater Band dieser Reihe dafür vorzusehen ist. Bis zu dessen Fertigstellung sei auf die Dokumentation früherer Modellversionen (REICHE 1991, REICHE und MÜLLER 1994) verwiesen.
Im folgenden soll nach einem Überblick über die Anwendungsmöglichkeiten und über die bereits durchgeführten Modellanwendungen eine grobe Beschreibung des Systems geliefert werden. Mit höherem Detailliertheitsgrad werden die Module dargestellt, die in jüngster Zeit entwickelt wurden und deren Beschreibung deshalb in der angegebenen Literatur noch fehlt.
Welche Fragestellungen lassen sich mit WASMOD bearbeiten?
Die Entwicklung und Fortentwicklung des Modellsystems umfaßt bis heute nahezu einen 10-jährigen Zeitraum. Während zu Beginn der Entwicklungen (FRÄNZLE et al. 1987, MÜLLER und REICHE 1990) die eindimensionale Beschreibung der Bodenpassage von Umweltchemikalien - vornehmlich Pestizide und Schwermetalle - im Mittelpunkt der Arbeiten stand, wurden in einer zweiten Phase Erweiterungen und Modifikationen in Hinblick auf die flächenhafte Modellanwendung durchgeführt (FRÄNZLE et al. 1991, REICHE 1991, REICHE und MÜLLER 1994). Im Rahmen des Forschungsvorhabens 'Ökosystemforschung im Bereich der Bornhöveder Seenkette' konnten seit 1992 auf der Grundlage zahlreicher Freiland-Meßergebnisse wesentliche Schritte zur Modellüberprüfung begonnen sowie wichtige Ergänzungen und Verbesserungen eingeführt werden. Diese beziehen sich u.a. auf die Entwicklung von Programmen, mittels derer die gebietsbezogene Parameterisierung von Modellsimulationen auf der Grundlage eines Geographischen Informationssystems weitgehend automatisiert ablaufen können (FLEISCHMANN 1992, REICHE 1994). Auf der Ebene der Prozeßbeschreibung sind folgende Erweiterungen hervorzuheben:
- verbesserte Modellierung der Grundwasserdynamik für grundwassernahe Standorte
- Integration der Humusdynamik
- Dynamisierung des Phänologieverlaufs und Darstellung der Nährstoff- und Assimilatverteilung in unterschiedlichen Pflanzenkompartimenten.
Darüber hinaus wurden Arbeiten zur Erstellung einer anwenderfreundlichen Bedienungsoberfläche mit fester Anbindung an das Datenbanksystem ORACLE durchgeführt (HOSENFELD 1992).
Eine Zusammenstellung der auf unterschiedlichen Raumebenen modellierten Prozesse (siehe Tabelle 1) soll zeigen, für welche Fragestellungen sich der Einsatz dieses Simulationswerkzeuges lohnt. Zu aller erst kommen Modellanwendungen im Rahmen wissenschaftlicher Studien in Frage: häufig lassen sich aus Praktikabilitäts- bzw. Kostengründen nicht alle für die Bearbeitung der jeweiligen Fragestellung erforderlichen Detailinformationen durch Freilandmessungen erheben; die Inanspruchnahme von simulierten Werten kann wichtige Lücken schließen und essentiell für die Ergebnisinterpretation sein. Weiterhin bietet das Modellsystem die Möglichkeit, über Jahrzehnte ablaufende Langzeitentwicklungen in Abhängigkeit von Stoffeinträgen, Bearbeitungsmaßnahmen und Klimabedingungen abzuschätzen (Auf- und Abbau von Nährstoffpools, Veränderungen des Kohlenstoffvorrats und der mikrobiologischen Aktivität; Veränderung bodenphysikalischer und -chemischer Eigenschaften). Eine geplante Koppelung mit Simulationsmodellen, die die Anpassung der Vegetationszusammensetzung an die jeweiligen Standortverhältnisse beschreiben, soll die Möglichkeit bieten, die Langfristentwicklung unterschiedlicher Ökosysteme in Abhängigkeit von der Standortausstattung und von externen Randbedingungen (Klima, Nutzung, Stoffeinträge) abzubilden. Auf der Grundlage solcher Ökosystem-Simulationen können gegebenenfalls verschiedene Hypothesen der Ökosystem- theorie überprüft werden.
Tabelle 1 : Liste der berücksichtigten Einzelprozesse
|
A
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13. |
als Standortmodell
Simulation der Bodenwasserdynamik (inkl. Interzeption, Evapotranspiration, Infiltration)
Simulation des Drän-Abflusses
Simplifizierte Simulation des Grundwasserabflusses und des Grundwasserflurabstandes
Simulation des vertikalen Transportes gelöster Stoffe in Böden (inkl. Aufnahme durch Pflanzenwurzeln)
Simulation der Ad- und Desorptionsdynamik von Stoffen in Böden
Berechnung des vertikalen Bodenwärmetransports
Simulation der Kohlenstoff-Umsetzungsprozesse im Boden (Humifizierung, Mineralisation inkl. Quantifizierung der CO2-Freisetzung)
Berechnung der mikrobiell gesteuerten Stickstoffumsetzungsprozesse im Boden und an der Bodenoberfläche (N-Ammonifizierung, N-Nitrifizierung, N-Denitrifikation, N-Immobilisierung)
Berechnung der gasförmigen NH4-N-Verluste
Berechnung des lateralen Transportes gelöster Stoffe durch die gesättigte Zone
Berechnung des Transportes gelöster Stoffe mit dem Dränwasser
Abschätzung langfristiger Veränderungen der Wasserleitfähigkeit und des Wasserhaltevermögens in Abhängigkeit von der Humusdynamik
Quantifizierung der N- und C-Akkumulation unterschiedlicher Pflanzenkompartimente |
|
B
1.
2.
3.
|
als Gebietsmodell auf der Grundlage der Standortmodellierung
Simulation des Oberflächenabflusses vom Hang bis in den Vorfluter bzw. in abflußlose Senken
Berechnung von flächenbezogenen Wasser- und Stickstoffbilanzen mit hierarchisiertem Flächenbezug von der 'kleinsten Geometrie' (definiert durch einheitliche Vegetation, Relief- und Bodenparameterisierung) über Einzelschläge, Teileinzugsgebiete bis zum Gesamteinzugsgebiet.
Berechnung von Abflußmengen und Stickstofffrachten als Eintrag in Gewässer und Gewässerteilabschnitte in unterschiedlicher zeitlicher Auflösung |
Ein wesentliches Entwicklungsziel ist aber auch die Anwendbarmachung für Fragen, die im Rahmen von gebietsbezogenen Planungsverfahren auftreten: z.B. Formulierung von Nutzungsauflagen für empfindliche Standorte, Ausweisung von Flächen, die aufgrund gegebener Ausstattung für Extensivierungsmaßnahmen in Frage kommen, Testung von geplanten Nutzungs- änderungen durch Szenarien-Simulationen. In diesem Bereich soll eine Weiterentwicklung des Systems die selbständige Formulierung von Nutzungsszenarien ermöglichen. Damit wäre dem Landschaftsmanagement ein Werkzeug in die Hand gelegt, mit welchem automatisiert nach Vorgabe von Nutzungs- und Umweltqualitätszielen Planungsvorschläge erarbeitet werden.
Wie die folgende Auflistung zeigt, wurde das Modellsystem im Rahmen der ökologischen Forschung bis heute innerhalb eines weiten Anwendungsfeldes genutzt:
- Abschätzungen zur Bodenpassage von Umweltchemikalien unter unterschiedlichen Boden- und Klimabedingungen (VETTER 1989, FRÄNZLE et al. 1987, MÜLLER 1987, HERTLING 1990, WITTKEMPER 1995)
- Temperatur- und Feuchteberechnungen im Rahmen von Untersuchungen zur Aktivität von Bodenmikroben (HALUSZCAK et al. 1991, WILLNOW 1993, KUTSCH 1994)
- Simulationsrechnungen zur Abschätzung von Dränwassermengen (SCHÜTT 1992)
- Bilanzierung von Wasser- und Stickstofffrachten in Grund- und Oberflächenwässer des Einzugsgebiets der Schmalenseefelder Au (FRÄNZLE et al. 1991, REICHE 1991).
- Bilanzierung von Wasser- und Stickstofffrachten in Grund- und Oberflächenwässer des Einzugsgebiets des Belauer Sees (REICHE 1994, SCHIMMING et al. 1995).
- Modellrechnungen zur Grundwasserdynamik von Feuchtgrünlandstandorten (SCHRAUTZER et al. 1995)
- Modellrechnungen zur Auswirkung kleinräumiger Standort-Heterogenitäten auf den Wasser- und Stickstoffhaushalt (REICHE und SCHLEUSS 1992, KERRINNES 1994, REICHE et al. 1994).
- Modellrechnungen zum Stickstoffhaushalt von Waldökosystemen (REICHE 1995).
- Modellrechnungen zum Wasser- und Stickstoffhaushalt von Acker-Ökosystemen unter veränderten Klimabedingungen (HÖRMANN et al. 1995, REICHE et al. 1995)
Während der gesamten Entwicklungszeit entfiel ein großer Teil des Arbeitsaufwandes auf den Abgleich von Modellresultaten mit Meßergebnissen (z.B. FRÄNZLE et al. 1987, REICHE 1991, SCHIMMING et al. 1995). Eine umfassende Studie zum Wasser- und Stoffhaushalt einer ca. 60 ha großen, drainierten Ackerfläche wird Ende des Jahre 1995 abgeschlossen sein und soll einen Vergleich zwischen simulierten und den im Dränabfluß gemessenen Stoff- und Wasserfrachten liefern (GÖBEL, i.V.). Die laufenden Arbeiten beziehen sich u.a. auf Simulationsrechnungen für das Gesamt-Einzugsgebiet der Bornhöveder Seenkette und für ein Teileinzugsgebiet der Stör (Osterau). Neben Berechnungen zum Wasser- und Stickstoffhaushalt sollen Berechnungen zum Protonenhaushalt und Abschätzungen zum Phosphateintrag in Oberflächenwässer durchgeführt werden.
Ein Modellüberblick
Der modulare Aufbau des Modells WASMOD wird in dem vereinfachten Konzeptschema in Abbildung 1 dargestellt. Vom Hauptprogramm aus wird die Ein- und Ausgabe, sowie die Prozeßsteuerung organisiert. Dabei werden unterschiedliche Prozesse, je nach Raumbezug und Effektivität, in unterschiedlichen Zeitintervallen aufgerufen. Beispielsweise erfolgt die Berechnung des Phänologieverlaufs nur einmal für jedes zu simulierende Jahr und gilt für das Gesamtgebiet. Ebenso werden die sich langfristig verändernden Parameter, wie die pF- und kf-Funktionen, nur jährlich korrigiert. Schnell ablaufende Prozesse, wie die Bodenwasserbewegung werden im Minuten- bzw. Stundenrhythmus berechnet. Es wird generell zwischen vier Ökosystem-Kompartimenten unterschieden: Pflanzenbestand, Bodenkörper, Grundwasserkörper und Vorfluter.
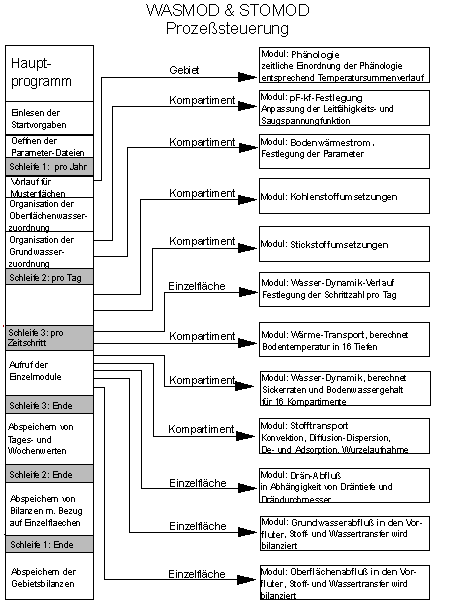
Abbildung 1: Prozeßsteuerung und Teilmodule des Modellsystems WASMOD
Modellierung der Bodenwasserdynamik
Um die Wasserdynamik in der Bodenzone abzubilden, wird die von bodenphysikalischen Kennwerten sowie von Witterungs- und Vegetationsbedingungen abhängige Verweildauer des Bodenwassers in einzelnen Tiefenstufen (Kompartimenten) bzw. seine ab- und aufwärtsgerichtete Bewegung zwischen diesen Kompartimenten berechnet. Vernachlässigt man die horizontale Wasserbewegung an der Bodenoberfläche (Oberflächenabfluß) und in unterschiedlichen Bodentiefen (Interflow), so läßt sich die Wasserbewegung durch die von der Kontinuitätsgleichung und dem Darcy-Gesetz abgeleitete allgemeine Bewegungsgleichung des Bodenwassers beschreiben:
|
(1) Bewegungsgleichung des Bodenwassers |
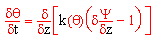
mit:
q = Wassergehalt
t = Zeit
k = Durchlässigkeitsbeiwert
y = Matrixpotential
z = vertikale Kompartimentmächtigkeit
Eine verbale Beschreibung der Gleichung 1 könnte folgendermaßen lauten: Die Änderung des Bodenwassergehalts pro Zeiteinheit hängt von den Veränderungen des Gradienten des Matrixpotentials entlang der vertikalen Raumachse z ab, welche die Fließrichtung darstellt. Sie wird wesentlich bestimmt durch die Größe des Durchlässigkeitsbeiwertes k (Leitfähigkeit).
In diese Gleichung gehen zwei für den Bodenwasserhaushalt wesentliche Größen ein: der Durchlässigkeitsbeiwert k (das Vermögen von Boden- oder Gesteinsschichten, Wasser zu leiten) und das Matrixpotential (Intensität der Wasserbindung). Dabei ist zu beachten, daß beide Größen nicht als Konstanten, sondern als Funktionen des Wassergehaltes anzusehen sind. Eine genaue Quantifizierung dieser Parameter läßt sich nur durch sehr aufwendige Labor- bzw. Feldmessungen erreichen. Das Modell WASMOD bietet die Möglichkeit, diese Funktionen in Abhängigkeit von der Korngrößenverteilung (Sand-, Schluff- und Tonanteil) und vom Humusgehalt abzuleiten. Es werden dabei Regressionsgleichungen verwendet, die auf einem umfangreichen, das Spektrum schleswig-holsteinischer Böden - mit Aunahme von Sandböden - weitgehend abdeckenden Datensatz beruhen (REICHE 1985, MÜLLER 1987, FRÄNZLE et al. 1987). Die Wassergehalts-Saugspannungszuordnung erfolgt über lineare Interpolation auf der Grundlage von 5 Stützstellen (Wassergehalt bei Matrixpotentialen von pF 0, pF 1.8, pF 2.5, pF 3.5, pF 4.2).
|
(2) Regressionsgleichung zur Ableitung der pF-Stützstellen |
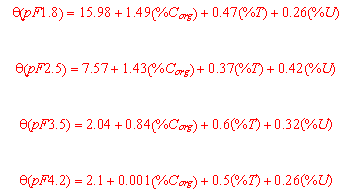
mit: % Corg = Gewichtsanteil an organischer Substanz
% Ton = Gewichtsanteil an Ton
% U = Gewichtsanteil an Schluff
q (pFx) = Wassergehalt bei pF = x
Die Wasserleitfähigkeitsfunktion wird in Abhängigkeit von der gesättigten Wasserleitfähigkeit (kf) nach Gleichung 3 berechnet, die auf der Grundlage einer großen Anzahl von Tensiometer- und Wassergehaltsmessungen abgeleitet wurde (s. FRÄNZLE et al. 1987, MÜLLER 1987, MÜLLER und REICHE 1990).
|
(3) Berechnung des Durchlässigkeitsbeiwertes |

mit:
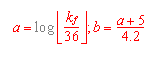
für kf <50
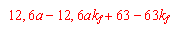
für kf >50 und <100
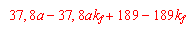
für kf >100 und <300
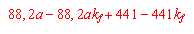
für kf >300 und <450
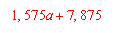
für kf >450 und <600
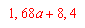
für kf >600
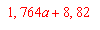
für 0<pF<1.8
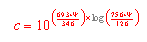
für pF>1.8
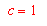
Teilt man eine Bodensäule in beliebig viele Kompartimente festgelegter Schichtdicken ein, so läßt sich auf der Grundlage der Differentialgleichung (1) nach Diskretisierung unter Anwendung der Finite-Differenzen-Methode die Bodenwasserbewegung durch ein numerisches, iterativ ablaufendes Rechenmodell beschreiben (DUYNISVELD 1984, BENECKE 1984). D.h. entsprechend der Gleichung 1 läßt sich der Gang des Bodenwassers berechnen, wenn man den Boden entsprechend seiner hydraulischen Eigenschaften in einzelne Tiefenstufen aufteilt und für diese Schichten im Minuten- bis Stundenabstand die Änderung des Wassergehalts berechnet. Dabei stellt jeweils der für einen Zeitschritt berechnete Endzustand (Bodenwassergehalt, Matrixpotential und Durchlässigkeitsbeiwert) den Anfangzustand für den folgenden Schritt dar.
Bei der Beschreibung der Bodenwasserdynamik ist die Einbeziehung des Wassertransfers von der Bodenoberfläche in das oberste Bodenkompartiment (obere Randbedingung), der Pflanzendecke sowie des Übergang zum Grundwasser (untere Randbedingung) notwendig. Um eine praktikable Anbindung der Berechnung des Bodenwassers an die Grundwasserdynamik zu erreichen, wurde ein Berechnungsverfahren angewendet, bei dem die Schichtdicke des untersten, über dem Grundwasser liegenden Kompartimentes variabel gehalten wird. Der Potentialgradient wird als Differenz zwischen dem aktuellen Matrixpotential und dem sich unter stationären Bedingungen in Abhängigkeit zur Grundwassertiefe einstellenden Potential berechnet, so daß die Flußrate in das unterste Kompartiment, also in den Grundwasserkörper, nach Gleichung 4 berechnet werden kann:
|
(4) Grundwasserneubildungsrate |
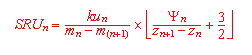
mit:
SRU = Sickerrate in das Grundwasser
ku = Durchlässigkeitsbeiwert (ungesättigt)
y = Matrixpotential
m = Ortskoordinate der Kompartimentmitte
z = Ortskoordinate der oberen Kompartimentgrenze
|
(5) Berechnung der Grundwasserhöhe |
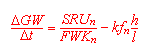
mit:
DGW = Veränderung der Grundwasserhöhe
t = Zeit
SRU = Sickerrate in das Grundwasser
FWK = auffüllbarer Porenraum (freie Wasserkapazität)
h = Höhe über dem Vorfluter
l = Entfernung zum Vorfluter
kf = Leitfähigkeit (gesättigt)
Für Standorte mit hohen Gundwasserständen hat sich diese Methode als nicht zufriedenstellend erwiesen, da das unterste Kompartiment nur bis zu einer Mindest-Vertikalausdehnung (20 cm) schrumpfen kann, die Anzahl an Kompartimenten muß aus modellierungstechnischen Gründen innerhalb eines Simulationslaufes konstant bleiben (Standardanzahl = 15). D.h., wenn das Grundwasser weiter ansteigt, als die Summe aller Kompartimentmächtigkeiten (i. d. Regel 180 cm), würde der Grundwasserstand konstant gehalten bzw. - wie in früheren Modellversionen - in Abhängigkeit vom Sättigungsgrad einzelner Kompartimente auf die Höhe des obersten noch gesättigten Kompartimentes festgelegt. Diese Herangehensweise führte bei der Simulation grundwassernaher Standorte teilweise zu einem sprunghaften Abflußverhalten. Seit der WASMOD Version 3.9 und aufwärts wird für Standorte mit geringem Flurabstand mit einer optmierten Methode gerechnet. Dazu wird für den Fall, daß die Wassersättigung über die minimale Ausdehnungstiefe ansteigt, auf ein modifiziertes Berechnungsverfahren umgeschaltet. Zunächst werden die Einzelkompartimente in der Reihenfolge von unten nach oben auf ihren Wassersättigungsgrad hin überprüft. In Abhängigkeit von der Porensättigung oberhalb der Feldkapazität eines Kompartimentes wird dann auf die Höhe des Grundwasserstandes geschlossen.
|
(6) modifizierte Berechnung der Grundwasserhöhe bei grundwassernahen Standorten |
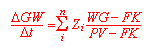
mit:
PV = Porenvolumen
FK = Wassergehalt bei Feldkapazität
WG = aktueller Wassergehalt
Zi = Kompartimentmächtigkeit
Es werden hierbei nur die Kompartimente berücksichtig, bei denen vom untersten Kompartiment an ohne Unterbrechung der Wassergehalt die Feldkapazität überschreitet. Diese Vorgehensweise ermöglicht eine kontinuierliche Berechnung der Grundwasserdynamik bis an die Bodenoberfläche bzw. auch für Bereiche darüber, wenn nicht abfließendes Oberflächenwasser berücksichtigt werden muß.
Der Grundwasserabfluß wird in Anlehnung an die Darcy-Gleichung stark vereinfachend in Abhängigkeit vom Gefälle des Grundwassers, bezogen auf die Lage des zu berechnenden Punktes, und von der Durchlässigkeit des Grundwasserleiters bestimmt, wobei der Zufluß aus anliegenden Gebieten (Basis-Strom) als konstant angenommen wird.
Das Rechenmodell WASMOD bietet auch die Möglichkeit, den Wasserabfluß aus einem beliebigen Kompartiment als Dränabfluß abzuschätzen. Als Berechnungsgrundlage wird ebenfalls die Gleichung 5 herangezogen, wobei der Dränabfluß in Abhängigkeit vom mittleren Dränabstand, der Dräntiefe, der mittleren berechneten Aufwölbung zwischen den Dränen und den k-Werten der wassergesättigten Schichten ermittelt wird. Hierzu wird der Drän analog zum Vorfluter beschrieben. D.h., es wird davon ausgegangen, daß der minimale Grundwasserstand direkt am Drain auftritt, während der maximale Grundwasser- (bzw. Stauwasserstand) sich bei maximalem Dränabstand, also zwischen zwei Dränen befindet. Es wird vereinfachend angenommen, daß sich der Grundwasserabstand linear zum Dränabstand verhält, so daß bei einer Entfernung von 0.25 x Dränabstand mit einem mittleren Grundwasserstand gerechnet werden kann (Abb. 2).
Bei der modellhaften Formulierung der an und über der Bodenoberfläche ablaufenden Prozesse muß neben dem Niederschlag die Interzeption (der Anteil des Niederschlags, der an oberirdischen Pflanzenteilen haften bleibt), die Evapotranspiration (Verdunstung) sowie temporär auftretendes Oberflächenwasser Berücksichtigung finden. Zur Kennzeichnung des täglichen Niederschlags werden Meßwerte eingelesen. Der Tagesgang des Niederschlages kann in Abhängigkeit von der Großwetterlage 3 Formen annehmen: Dauerregen bei Warmfrontlage (es regnet 8 Stunden pro Tag), viele kurze Regenschauer bei Kaltfrontlage, Starkregenereignis bei Gewitterlage. Die Wetterlagen werden jeweils vom Temperaturgang und von der Luftfeuchtigkeit abgeleitet.
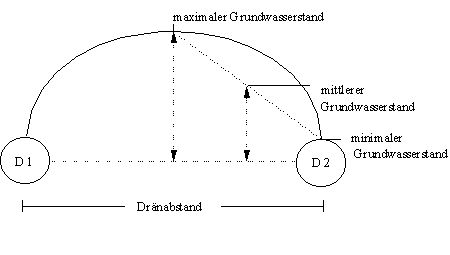
Dq = - (Dräntiefe - Grundwasserabstand)/(0.25 x (Dränabstand) x kF < for y < 63.3 cm
Abbildung 2: Schematische Übersicht zur Berechnung des Dränabflusses
Der Interzeptionsverlust wird anhand der von HOYNINGEN-HUENE (1983) empirisch ermittelten Gleichungen in Abhängigkeit vom Blattflächenindex LAI (Verhältnis zwischen Oberfläche der Pflanzenteile und der von der Pflanze bedeckten Grundfläche) berechnet.
|
(7) Interzeptionsverlust (Ni) |
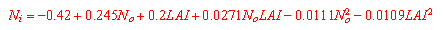
mit:
Ni = Interzeptionsverlust als Anteil des Gesamtniederschlags
No = Freilandniederschlag
LAI = Blattflächenindex
Der Interzeptionsverlust steigt in Abhängigkeit von der Niederschlagsmenge bis zu einer oberen Grenze, die durch die Gleichung 7 beschrieben wird.
|
(8) Interzeptionspotential |
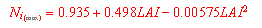
mit: Ni(max)= Grenzwert der Interzeptionskapazität
Der als Differenz des Freilandniederschlags und der Interzeptionsrate berechnete Bestandesniederschlag wird als Vorratsänderung zum Wassergehalt des obersten Kompartimentes hinzuaddiert, solange das Porenvolumen dieses Kompartimentes nicht überschritten ist. Dies kann dann der Fall sein, wenn bei grundwassernahen Böden hohe Wassereinträge zur vollständigen Sättigung der Bodensäule führen oder wenn aufgrund niedriger Durchlässigkeitsbeiwerte die Versickerung in die tieferen Kompartimente so langsam abläuft, da das oberste Kompartiment den Sättigungspunkt erreicht. Der Wasseranteil, der nicht infiltriert, wird bei niedriger Hangneigung bzw. dichtem Bewuchs als Oberflächenwasser für den folgenden Simulationszeitschritt gespeichert und kann bei entsprechender Abnahme des Bodenwassergehalts in die oberste Schicht infiltrieren. Steigt die berechnete Menge an nicht infiltriertem Wasser über eine von der jeweiligen Vegetationsdecke abhängige Höhe, so wird diese Wassermenge bei entsprechender Hangneigung (>2% Gefälle) als Oberflächenabfluß bilanziert. Um die Verdunstung zu berechnen, wird zunächst die potentielle Evapotranspiration (Verdunstung bei uneingeschränktem Wasservorrat) nach dem Verfahren von HAUDE (1954) ermittelt. Dazu ist die Kenntnis des Sättigungsdefizits der Atmosphäre (14) und der Lufttemperatur (14) in Form von Tageswerten erforderlich. Diese Parameter werden ebenso wie die tägliche Niederschlagssumme an vielen Stationen des Deutschen Wetterdienstes erhoben und sind damit mehr oder weniger flächendeckend verfügbar. Durch die Verwendung von empirisch gut abgesicherten, spezifischen, jeweils auf Entwicklungsstadien bezogenen Pflanzenfaktoren kann auf aufwendige Subprogramme zur Berechnung des Transpirationspotentials verzichtet werden (ERNSTBERGER 1987).
|
(9) potentielle Evapotranspiration (nach HAUDE) |
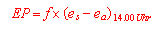
mit:
EP = potentielle Evapotranspiration
f = Faktor (abhängig vom Pflanzenart und Phänologie)
es-ea = Sättigungsdefizit der bodennahen Luftschicht
Als Alternativverfahren zur Berechnung der potentiellen Evapotranspiration wurde die Methode nach Turc-Wendling in das Modellsystem integriert. Dieser vereinfachte Penman Ansatz bietet die Möglichkeit, Verdunstungswerte in Abhängigkeit von der Strahlungssumme (Globalstrahlung in J/cm³) und dem Tagesdurchschnitt der Lufttemperatur zu berechnen. Vergleiche mit Meßwerten weisen diesem Verfahren eine hohe Genauigkeit aus. Die Methode bietet sich im Vergleich zum Haude-Verfahren insbesondere auch für küstennahe Standorte an, da hier eine Einbeziehung der Luftfeuchte (Sättigungsdampfdruck) nicht sinnvoll ist. Es hat sich gezeigt, daß die Resultate, die sich aus der Turc-Wendling Berechnung ergeben, im Durchschnitt höher liegen, als die der Haude Berechnung. Neuere Untersuchungen zur Genauigkeit der Niederschlagsmessungen zeigen, daß eine Korrektur in Abhängigkeit von Standorteigenschaften und Meßverfahren empfehlenswert ist. Der Korrekturfaktor liegt bei ebenen, von der Vegetation nicht beeinflußten Standorten bei 1.1, wenn Meßgefäße nach Hellmann zum Einsatz kommen.
|
(9b) Berechnung von ETp-Tageswerten nach dem Turc-Wendling-Verfahren
|
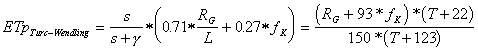
mit R=G Tagessumme der Globalstrahlung in J/cm2
T= Tagesmittel der Lufttemperatur in 2 m Höhe über Grund
s= Steigung der Sättigungsdampfdruckkurve in hPa/K
g= Psychrometerkonstante in hPa/K
f=K Küstenfaktor; im Küstenbereich von 50 km Breite als Mittelwert fK = 0.6 und sonst fK = 1.0
Die aktuelle Evapotranspiration wird in Abhängigkeit von der relativen Durchwurzelungsintensität als Funktion der Tiefe für einzelne Kompartimente in Anlehnung an BRAUN (1975) berechnet. Dabei wird vereinfachend nur für die obersten Kompartimente eine Evaporationsrate bestimmt; der Betrag der potentiellen Evapotranspiration wird hier um die Höhe des Interzeptionsverlustes reduziert. Die Wasserentzugsrate entspricht damit der potentiellen Evapotranspiration, wenn der Boden wassergesättigt ist, bzw. wenn Oberflächenwasser im vorausgegangenen Rechenschritt bilanziert wurde.
|
(10) aktuelle Evapotranspiration (nach BRAUN) |
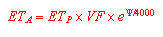
mit:
ETA = aktuelle Evapotranspiration
ETP = potentielle Evapotranspiration
VF = Vegetationsfaktor
y = Matrixpotential
Bei ungesättigten Verhältnissen wird dieser Betrag entsprechend der Höhe des als Verdunstungswiderstand anzusehenden Matrixpotentials reduziert.
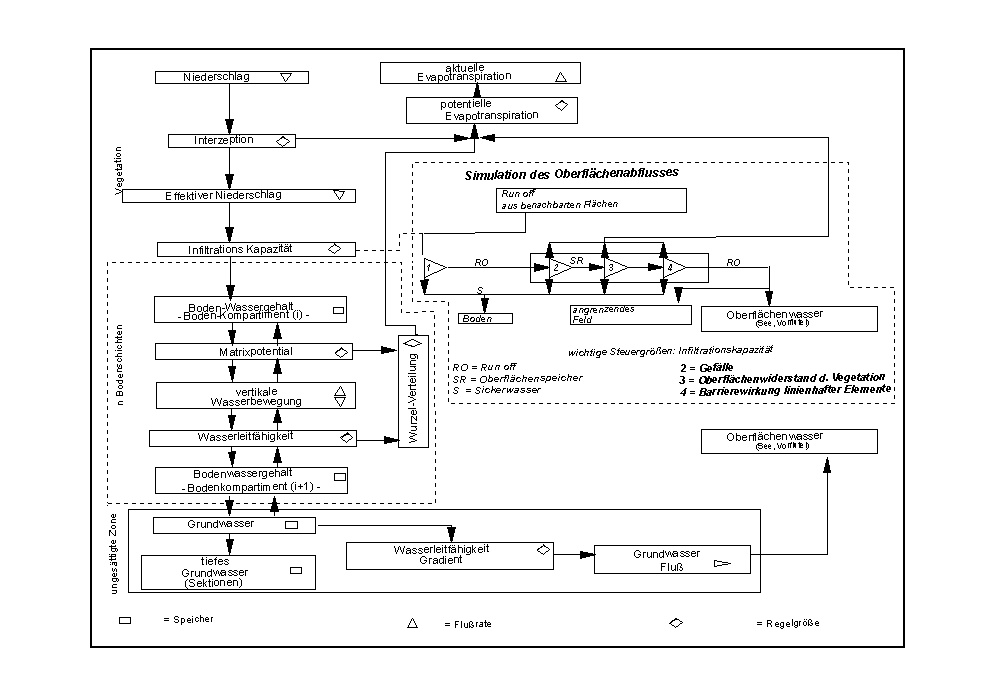
Abbildung 3 : Teilprozesse der Wasserhaushalts-Modellierung
Modellierung der Bodentemperatur
Der Wärmetransport im Boden läßt sich in Abhängigkeit von der Wärmeleitfähigkeit und unter Einbeziehung der Wärmekapazität (Cw) für unterschiedliche Bodenkompartimente durch die Wärmeleitgleichhung bechreiben. Dabei wird der durch die Wasserbewegung (q) verursachte konvektive Wärmetransport berücksichtigt.
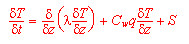
mit:
dT/dt = Veränderung der Temperatur pro Zeitintervall
dT/dz = vertikaler Temperaturgradient (vom oberen zum unteren Rand eines Kompartimentes
t = Zeitkoordinate
z = Ortsachse
S = Senkenterm
l = Temperaturleitfähigkeit
Beide Faktoren hängen im starken Maße vom Wassergehalt sowie mineralischen und nicht mineralischen Anteilen der Bodenmatrix ab. Als untere Randbedingung kann eine konstante bzw. in Abhängigkeit von der Jahresmitteltemperatur und dem Jahrestag in vorgegebenen Grenzen schwankende Temperatur angenommen werden. Es wird vereinfachend davon ausgegangen, daß die Tages-Maxima und -Minima der Bodenoberflächentemperatur mit jenen der bodennahen Luftschicht gleichgesetzt werden können. Der Tagesgang wird in Anlehnung an das von PATRON & LOGON (1980) beschriebene Modell berechnet.
Gleichung ?? wird für die Berechnung des Temperaturganges während der Nacht, Gleichung ?? für jenen während des Tages eingesetzt.
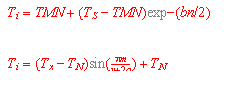
mit:
Ti = Temperatur zum Zeitpunkt i
TMN = Minimumtemperatur bei Nacht
TS = Temperatur
Tx = Temperatur
bn =
m =
y =
a =
Die Tages- und Nachtlängen werden als Funktionen des Jahrestages und des Breitengrades berechnet. Die Minimumtemperatur wird in Abhängigkeit vom Jahrestag der frühen Morgenstunden zugeordnet. Der Temperaturgang während des Tages wird durch eine verkürzte Sinus- funktion beschrieben, während die nächtliche Temperatur anhand einer Exponentialfunktion einzelnen Zeitpunkten zugeordnet wird.
Für die Berechnungen der mikrobiologisch geteuerten C- und N-Umsetzungsprozesse wird nur eine Tagesmitteltemperatur für jedes Bodenkompartiment benötigt. Das Bodentemperaturmodell wird unabhängig von der Schrittzahl des Teilmodells "Bodenwasserhaushalt" pro zu simulierenden Tag 6 mal aufgerufen. (Zeitschritt = 4 Stunden). Als zusätzliche Eingangsparameter werden neben den für einzelne Kompartimente berechneten Bodenwassergehalten und Sickerraten die Tages-Minimum- und Maximum-Temperatur benötigt. Die matrixabhängigen Teilkoeffizienten zur Bestimmung von Wärmeleitfähigkeit und -kapazität werden von den vorgegebenen Anteilen an Humus, Ton und Schluff sowie aus dem Trockenraumgewicht des Bodens in Anlehnung an PENNING DE FRIES & VAN LAAR (1982) abgeleitet.
Modellierung des Stofftransportes
Bei der modellhaften Beschreibung des Transports von in der Bodenlösung gelösten Stoffen sind drei Prozesse zu berücksichtigen: die Konvektion, die molekulare Diffusion und die hydrodynamische Dispersion. Diese Mechanismen lassen sich durch die folgende partielle Differentialgleichung beschreiben:
|
(11) vertikaler Stofftransport |
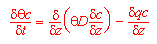
mit:
q = Wassergehalt
c = Konzentration in der Lösung
D = scheinbarer Diffusionskoeffizient
q = vertikaler Wasserfluß
z = Kompartimentmächtigkeit
t = Zeit
Während die molekulare Diffusion (Ausgleich von Konzentrationsunterschieden) durch die thermische Bewegung der Moleküle verursacht wird und auch ohne Wasserbewegung stattfindet, tritt die hydrodynamische Dispersion nur bei Wasserbewegung auf. Sie wird durch ungleichmäßige Fließgeschwindigkeiten bei der Bewegung einer Flüssigkeit durch poröse Medien verursacht, wobei unterschiedliche Porendurchmesser verschiedene Fließgeschwindigkeiten verursachen.
Neben der konvektiven Verlagerung (vertikale Bewegung), der Diffusion und der Dispersion werden auch Austauschprozesse mit dem Bodenkörper (De- und Adsorptionsprozesse) unter Einbeziehung einer mobilen und einer immobilen Wasserfraktion berücksichtigt (siehe Abb.3) .
Als wichtige Steuergrößen für die Beschreibung der Mineralisierung, der Nitrifikation und der Denitrifikation wird die Bodentemperatur durch Integration eines Bodentemperatur-Modells berechnet (s. REICHE 1991).
Die mikrobiologisch gesteuerten Prozesse des Stickstoffhaushalts, die in der Hauptsache im Auflage- und Ah/Ap-Horizont ablaufen, stehen wie die pflanzenphysiologischen Umsetzungen in enger Verbindung zur Kohlenstoffdynamik. Aus diesem Grunde sind die Teilmodelle zur Berechnung der N-Mineralisation und Immobilisierung an ein Teilmodell gekoppelt, welches in Anlehnung an HANSEN et al. (1990) die Umsetzung der organischen Substanz in Böden simuliert. Dabei wird die organische Substanz des Bodens aufbauend auf ein Konzept von JENKINSON et al. (1987) in 3 Haupt-Pools zu unterteilt:
- im Boden längerfristig lagernde organische Substanz (SOM)
- mikrobielle Biomasse (BOM)
- zugefügte, frische organische Substanz (AOM)
Weiterhin erfolgt eine Unterteilung in jeweils 2 Teil-Pools. Dabei wird davon ausgegangen, daß die einzelnen Pools der toten organischen Substanz (AOM, SOM) ein weites Spektrum unterschiedlicher chemischer und physikalischer Stabilität aufweisen. Dieses Spektrum wird im Modell vereinfachend durch jeweils 2 Teil-Pools so abgebildet, daß diese die schnell zersetzbare und die langsam zersetzbare Fraktion repräsentieren. Deren Mischungsverhältnis bestimmt damit die Dekompositionsrate entscheidend.
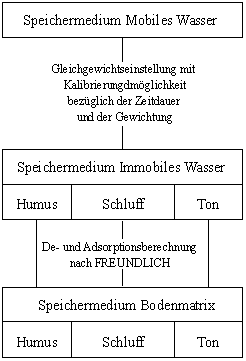
Abbildung 4 : Teilmodul De- und Adsorption von Stoffen unter Berücksichtigung einer immobilen Wasser fraktion
Die mikrobielle Biomasse wird ebenso in Form von zwei Kohlenstoff-Pools abgebildet. Hierdurch soll das Spektrum unterschiedlicher Mikroorganismen in Abhängigkeit von ihrer Populationsdynamik repräsentiert werden. Auf der einen Seite stehen die Spezies, die an eher schwer zersetzbare Substrate angepaßt sind, somit längerfristig stabile Nahrungsverhältnisse vorfinden und deshalb durch eine geringe Populationsdynamik gekennzeichnet sind, auf der anderen Seite jene, die leicht zersetzbares Material bevorzugen und sich durch eine schnelle Reaktion auf veränderte Nahrungsverhältnisse auszeichnen.
Die Dekompositionsprozesse werden als Kinetik erster Ordnung beschrieben:
|
(12) Kohlenstoff-Mineralisation |

Der Koeffizient K wird zunächst bezogen auf Standard-Bedingungen (Tongehalt = 0 %, Temperatur = 10° C, Wassergehalt bei pF 1.8, pH-Wert > 5) für die einzelnen Pool-Transferraten festgelegt und während der Simulation entsprechend der für einzelne Zeitschritte berechneten abiotischen Faktoren (Bodenwassergehalt, Temperatur, Acidität und Tongehalt) modifiziert. Die Dynamik der mikrobiellen Biomasse wird zusätzlich durch Koeffizienten, die die geschätzte 'maintenance' und die Sterberate der Organismengruppen abbilden, gesteuert.
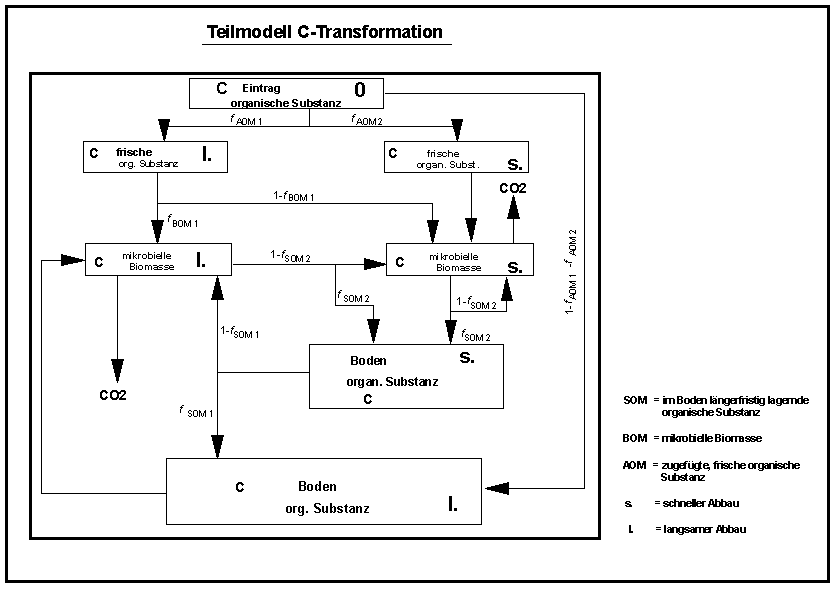
Abbildung 5 : Übersicht zu den Corg-Pools und ihren Umsetzungspfaden (nach HANSEN et al. 1990)

mit:
C = Kohlenstoffkonzentration im Boden (kg m-3)
z = Abbau- und Umsetzungsrate (kg C m-3 s-1)
E = Grad der Substratausnutzung
D = Sterberate (kg C m-3 s-1)
f = Partionierungsfaktor
t = Zeit (s)
IC = Eintrag an organischem Kohlenstoff (kg C m-3 )
ID = zeitliche Verteilung des Eintrags (kg C m-3 s-1) entsprechend der Funktion
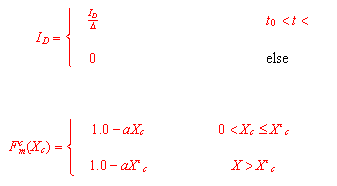
mit:
Fcm(Xc) = Tongehalt
Xc = Tongehalt (kg kg -1)
X`c = Tongehalt (0.25 kg kg -1)
a = Parameter (0.02)
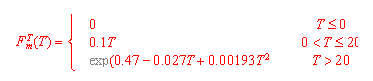
mit:
FTm(T) = der Bodentemperatur
T = Bodentemperatur
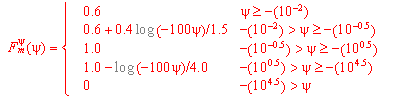
mit:
F
ym(y) = Bodenwassergehalt
y = Druckpotential des Bodenwassers (m H2O)

pH-Faktor:
pH > 4 : f pH = 1
pH < 4 > 3.2 4 < pH >3.2 : f pH = 0.5 + (pH -3) / 2
pH < 3.2 > 3.2 > pH < 2.2 : f pH = (0.5 x (pH - 22 )2
pH < 2.2 : f pH = 0
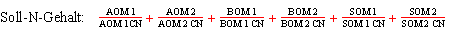
mit:
AOM 1 CN = unterschiedlich je nach Eintrag
AOM 2 CN = 30
BOM 1 CN = 6
BOM 2 CN = 10
SOM 1 CN = 11 (bei Acker) / 22 (bei Wald)
SOM 2 CN = 11 (bei Acker) / 15 (bei Wald)
Die Stickstoffmineralisation läßt sich so als Summe aller Kohlenstoff-Pool-Übergänge unter Zugrundelegung fester C/N-Verhältnisse von der C-Dynamik ableiten. Überwiegt die CO2- Freisetzung, so wird auch eine Ammonium-Freisetzung berechnet; in Phasen, in denen organische Substanz mit weiten C/N-Verhältnissen in die mikrobielle Biomasse, die sich durch enge C/N-Verhältnisse auszeichnet, übergeht, kann eine Immobilisierung von Ammonium bzw. Nitrat simuliert werden. Liegt mineralischer Stickstoff nicht in ausreichender Menge vor, kommt es zu einer entsprechenden Verminderung der Kohlenstoff-Umsetzungsraten.
Nitrifikation, Denitrifikation und Ammoniak-Verdunstung werden nach den Gleichungen 12, 13 und 14 berechnet. In Anlehnung an HOFFMANN (1988).
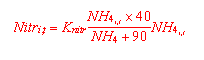
mit:
Nitr = Nitrifikationsrate
K = Faktor
NH4 = Ammoniumgehalt
i = Ortskoordinate
t = Zeitkoordinate
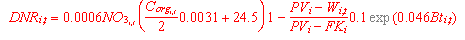
mit:
DNR = Denitrifikationsrate
NO3 = Nitratgehalt
Corg = organischer Kohlenstoffgehalt
PV = Porenvolumen
WG = Wassergehalt
FK = Feldkapazität
Bt = Bodentemperatur (°C)
|
(15) Ammoniak-Verdunstung |
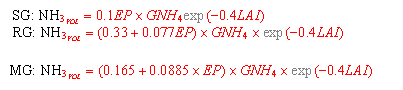
mit:
SG = Schweinegülle
RG = Rindergülle
MG = Mischgülle
LAI = Blattflächenindex
EP = potentielle Evapotranspiration
GNH4 = Ammoniumanteil der Gülle
Bei der Berechnung der Nitrifikation (verändert nach JONES and KINREY 1986) geht als Reduktionsfaktor K jeweils das Minimum der nach HAGIN and AMBERGER (1974) berechneten Temperatur-, Wassergehalts- und pH-Funktion ein. Bei dem in Anlehnung an ROLSTON and BROADBENT (1977) eingesetzten Verfahren zur Abschätzung der Denitrifikationsrate wird der Stickstoffverlust (DNR) in Abhängigkeit vom organischen Kohlenstoffgehalt, der Bodendichte, und Bodentemperatur sowie mit Hilfe einer von JONES and KINREY (1986) übernommenen Wassergehaltsfunktion berechnet. Es werden folgende organische bzw. mineralische N-Eintragsformen berücksichtigt: Ammonium-Dünger, Nitratdünger, Kalkammonsalpeter (50 % NO3, 50 % NH4), Rindergülle, Schweinegülle, Mischgülle, atmosphärische Deposition (60 % NH4, 40 % NO3).
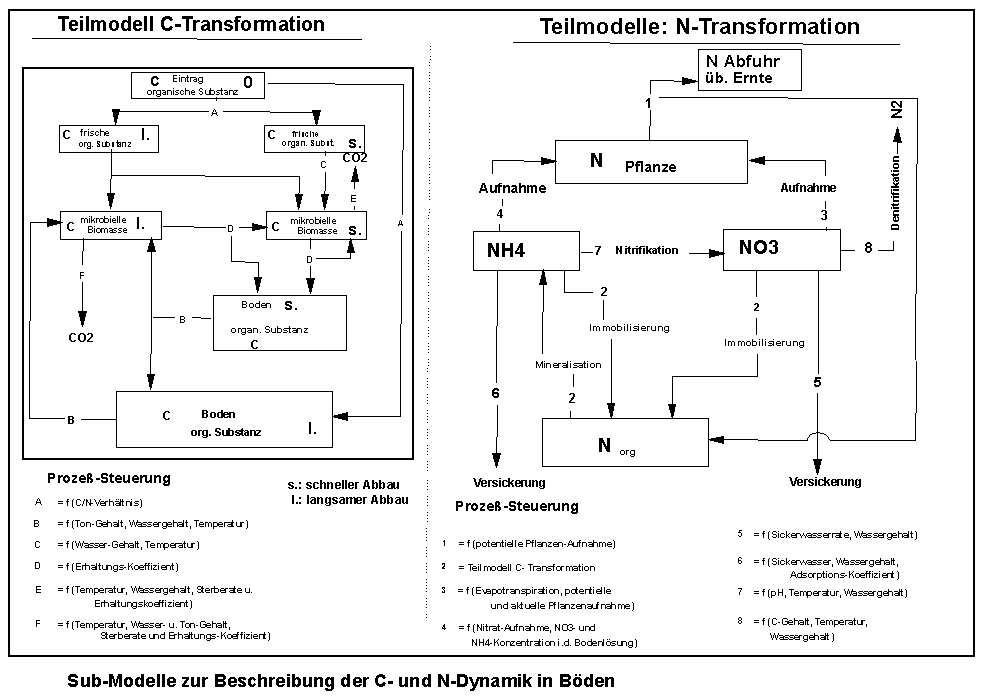
Abbildung 6 : Modellierte Teilprozesse zum Kohlenstoff- und Stickstoffhaushalt
Dynamisierung der Phänologie
Eine Reihe von vegetationsabhängigen Modellvariablen (Durchwurzelungstiefe, HAUDE-Faktor, Blattflächenindex) wurde in früheren Modellversionen in Form von Tabellenfunktionen eingelesen und konstant gehalten. Es hat sich gezeigt, daß für viele Fragestellungen diese Vorgehensweise unbefriedigend ist. Eine Anbindung von hoch differenzierten Pflanzenwachstumsmodellen ist für das Modellsystem zur Zeit allerdings schon deshalb nicht sinnvoll, weil es bei weitem nicht für alle flächenhaft vorkommenden Pflanzen- und Kulturarten Modellösungen gibt und weil andererseits die Parameterisierung solcher Modelle in der Regel kaum überwindbare Schwierigkeiten mit sich führt. Aus diesem Grunde ist weiterhin eine Beschränkung auf wenige - für die Wasser- und Stoffdynamik von Standorten unterschiedlicher Vegetationsausstattung charakteristische - Parameter sinnvoll.
Die verwendeten Größen sind zeitabhängige Angaben zur Durchwurzelungstiefe, zum LAI, zum Transpirationsvermögen, zum Nährstoffaufnahmevermögen und zu einzelnen landwirtschaftlichen Berarbeitungsmaßnahmen. Ein Schritt zur Dynamisierung dieser Größen wurde unternommen, indem sie in Abhängigkeit vom Jahrestemperaturgang - einem mittleren phänologischen Verlauf gegenübergestellt - zeitlich verschoben werden. Dazu wurde ein Phänologie-Datensatz des Deutschen Wetterdienstes (Beinhauer, frdl. Mittlg.), der wichtige landwirtschaftliche Kultur- und Zeigerarten (Schneeglöckchen, Hasel etc.) umfaßt, ausgewertet. Auf der Grundlage eines dreißig Jahre umfassenden Wetterdatensatzes (HEUWURTL 1995) konnte ein nach Leit-Arten differenzierter mittlerer Phänologieverlauf definiert und die für Einzeljahre festgestellten Abweichungen in Beziehung zu Abweichungen der mittleren Temperatursummen (Tagesmaximum) beschrieben werden (siehe Tab.2).
Die Berechnung der zeitlichen Verschiebung des Phänologieablaufes vom mittleren Verlauf (bezogen auf schleswig-holsteinische Beobachtungen) ergibt sich aus folgender Gleichung:
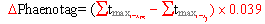
mit
D Phaenotag = Abweichung vom mittleren Phänologieverlauf in Tagen
S tmaxi-x = S des Tagesmax.-Temperaturen berechnet vom 1. Februar bis Tag x
m = über 30 Jahre gemittelter Witterungsverlauf (Tageswerte)
j = Witterungsverlauf (Tageswerte) des aktuell zu berechnenden Jahres
Tabelle 2 : Summen der Tages-Temperatur-Maxima berechnet als langjährige Mittel (1960-1990)
|
Tag im Jahr |
Summe der Tages-
Temperatur-Maxima |
Tag im Jahr |
Summe der Tages- Temperatur-Maxima |
|
1 |
0 |
182,00 |
1842 |
|
16 |
0 |
197,00 |
2163 |
|
32 |
8 |
213,00 |
2508 |
|
47 |
62 |
228,00 |
2843 |
|
60 |
113 |
244,00 |
3175 |
|
75 |
206 |
259,00 |
3457 |
|
91 |
342 |
274,00 |
3711 |
|
106 |
503 |
289,00 |
3933 |
|
121 |
703 |
305,00 |
4116 |
|
136 |
950 |
320,00 |
4244 |
|
152 |
1235 |
335,00 |
4337 |
|
167 |
1534 |
350,00 |
4404 |
Stickstoffaufnahme durch die Pflanzenwurzeln
Die Beschreibung pflanzenphysiologischer Teilprozesse erfolgt im Modell "WASMOD" teilweise auf eine sehr vereinfachende Weise. Wie weiter oben beschrieben, wird in der sogenannten "Phaeno-Datei" die Durchwurzelungstiefe, die Transpirationskapazität und der Blattflächenindex für unterschiedliche Teilräume eines mittleren Jahresverklaufes vorgesehen. Für Einzeljahre wird dieser Verlauf auf der Grundlage des Verhältnisses der aktuellen Temperatursummen den mittleren Temperatursummen angepaßt. Die Abschätzung der N-Aufnahme durch die Pflanzenwurzeln wird grundsätzlich aus den Größen "Wasserentnahme durch Transpiration" und "NO3-Konzentration" jeweils kompartimentbezogen vorgenommen. Pflanzen sind in der Lage, durch ein flexibles Feinwurzelwachstum gezielt in den Substratbereichen Nährstoffe aufzunehmen, wo diese in hohem Maße zur Verfügung stehen. D.h. die Nährstoffaufnahme findet auch "bedarfsorientiert" statt. Dem wird Rechnung getragen, indem eine art- bzw. sortenspezifische Angabe zur N-Aufnahmekapazität Berücksichtigung findet.
Solange die Differenz zwischen Aufnahmekapazität und aufgenommener Menge hoch ist, wird die aktuelle N-Aufnahme überproportional zum Transpirationsstrom berechnet. Ist die Aufnahmekapazität überschritten, wird keine weitere Aufnahme mehr kalkuliert. Die Aufnahmekapazität kann sich bei Trockenstreß reduzieren.
D
pflmaxi = pflmax i-1 x 1 - (0.9 - ndry/10)ndry
mit:
pflmax = maximale N-Aufnahmekapazität der Pflanzen
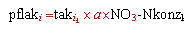
mit:
pflaki = aktuelle N-Aufnahme der Pflanzen zum Zeitpunkt i
takik = Transpirationsrate zum Zeitpunkt i im Kompartiment k
NO3 -Nkonzk = Nitrat-N-Konzentration im Kompartiment k
a = Anpassungsfaktor (pflanzenspezifisch)
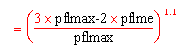
pflme =
S pflak1,i
Wasserfaktor
Zur Berechnung der unterschiedlichen C-Aufnahmekapazitäten der photosynthetisch aktiven bzw. nicht-aktiven Pflanzenteile findet weiterhin der Wasserfaktor Berücksichtigung, indem die Anzahl der Trockenwochen (ndry) wie folgt für Blätter (wblfak) und Stamm (wstfak) getrennt bestimmt wird:
wblfak = (1-ndry)/10 und
wstfak = (1-ndry/10)2
Aufteilung von Kohlenstoff und Stickstoff in pflanzenbezogene Teilspeicher
In früheren WASMOD-Versionen wurde das Pflanzenwachstum und die Verteilung der Assimilate bzw. der aufgenommenen Nährstoffe (Stickstoff) sehr stark vereinfacht dargestellt, indem die gesamte Pflanze durch jeweils nur eine stoffbezogene Speichervariable abgebildet wurde (s.o.). Dieser Ansatz bietet wenig Möglichkeiten, die Rückführung von Biomasse auf Bodenoberfläche bzw. in den Boden auch nur annähernd plausibel abzubilden. Aus diesem Grunde wurde die Anzahl der pflanzenbezogenen Speicher auf 3 erhöht. Diese teilen sich folgendermaßen auf:
Pflanzenspeicher 1: Haupternteprodukt
Hiebei handelt sich im Fall von landwirtschaftlichen Nutzpflanzen um jene Pflanzenteile, die in erster Linie über die Ernte einer Nutzung als Futter- bzw. Lebensmittel dem System entzogen werden. Bei Getreide ist es das Korn, bei Grünland die oberirische Biomasse (ohne Grasnarbe). Bei Mais wird die gesamte oberirdische Biomasse (bis auf einen geringen Ernterestanteil) dieser Fraktion zugerechnet. Bei Rüben und Kartoffeln wird diese Poolgröße durch die Rüben- bzw. die Knollenmenge abgbildet. Im Falle von Bäumen werden die Fruchtanteile und die Blätter durch diese Fraktion repräsentiert.
Pflanzenspeicher 2: oberirdische Pflanzenteile 2
Zu dieser Fraktion gehören alle Pflanzenteile, die oberhalb der Erdoberfläche anzutreffen, sind, die aber nicht zur Fraktion 1 gehören. Im Fall von Getreide handelt es sich dabei um das Stroh und die Stoppeln, im Falle von Rüben um das Rübenblatt u.s.w.. Bei Bäumen werden Stamm- und Astholz dieser Fraktion zugerechnet.
Pflanzenspeicher 3: unterirdische Pflanzenteile
Zu dieser Fraktion gehören alle Pflanzenteile, die vorher nicht der Fraktion 1 onder 2 zugerechnet wurden.
Angaben zu einer potentiell erreichbaren Biomasse sowie zur Aufteilung der Biomasse und der Nährstoffe enthält die Datei Pflanze:
|
Code Nr. |
TS |
NEP |
PEP |
ERT |
O |
ON |
OP |
W |
WN |
WG |
OG |
|
211000 |
25 |
0.47 |
0.12 |
176 |
0.2 |
0.21 |
0.12 |
0.5 |
0.47 |
3 |
5 |
|
211101 |
25 |
0.47 |
0.12 |
176 |
0.2 |
0.21 |
0.12 |
0.5 |
0.47 |
3 |
5 |
|
211110 |
17 |
0.42 |
0.17 |
176 |
0.1 |
0.47 |
0.17 |
0.6 |
0.1 |
3 |
5 |
|
211210 |
17 |
0.42 |
0.17 |
176 |
0.2 |
0.31 |
0.12 |
0.5 |
0.47 |
3 |
5 |
|
211220 |
17 |
0.32 |
0.12 |
176 |
0.2 |
0.31 |
0.12 |
0.6 |
0.1 |
3 |
5 |
|
211310 |
17 |
0.32 |
0.12 |
176 |
0.2 |
0.21 |
0.17 |
0.6 |
0.47 |
3 |
5 |
|
211320 |
17 |
0.42 |
0.17 |
176 |
0.1 |
0.47 |
0.17 |
0.6 |
0.1 |
3 |
5 |
|
211410 |
17 |
0.12 |
0.12 |
176 |
0.4 |
0.12 |
0.12 |
0.6 |
0.1 |
3 |
5 |
|
211510 |
17 |
0.22 |
0.12 |
176 |
0.4 |
0.12 |
0.12 |
0.6 |
0.1 |
3 |
5 |
|
212201 |
22 |
0.5 |
0.15 |
176 |
0.1 |
0.5 |
0.15 |
0.6 |
0.1 |
3 |
5 |
|
212202 |
22 |
0.5 |
0.15 |
176 |
0.1 |
0.5 |
0.15 |
0.6 |
0.1 |
3 |
5 |
|
213101 |
86 |
2 |
0.85 |
100 |
0.9 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213103 |
86 |
2 |
0.85 |
100 |
0.9 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213210 |
86 |
1.4 |
0.85 |
70 |
1.1 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213212 |
86 |
1.7 |
0.85 |
90 |
1 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213214 |
86 |
1.7 |
0.85 |
90 |
1 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213220 |
86 |
1.7 |
0.85 |
70 |
1.1 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213300 |
22 |
0.35 |
0.13 |
700 |
0.1 |
0.35 |
0.13 |
0.08 |
0.13 |
|
|
|
213303 |
86 |
1.6 |
0.85 |
80 |
1.4 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213304 |
86 |
1.6 |
0.85 |
80 |
1.4 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213321 |
86 |
1.6 |
0.85 |
80 |
1.4 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213350 |
86 |
1.8 |
0.85 |
80 |
0.9 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213401 |
86 |
1.6 |
0.85 |
75 |
1.2 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213402 |
86 |
1.6 |
0.85 |
75 |
1.2 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213421 |
86 |
1.6 |
0.85 |
75 |
1.2 |
0.55 |
0.3 |
0.3 |
0.1 |
|
|
|
213501 |
91 |
3 |
1.8 |
50 |
1.7 |
0.7 |
0.3 |
0.4 |
0.1 |
|
|
|
213502 |
91 |
3 |
1.8 |
50 |
1.7 |
0.7 |
0.3 |
0.4 |
0.1 |
|
|
|
213600 |
86 |
1.05 |
0.85 |
95 |
1.3 |
0.7 |
0.6 |
0.2 |
0.2 |
|
|
|
213602 |
28 |
0.35 |
0.2 |
500 |
0.1 |
0.25 |
0.2 |
0.04 |
0.2 |
|
|
|
213621 |
28 |
0.35 |
0.2 |
500 |
0.1 |
0.35 |
0.2 |
0.04 |
0.2 |
|
|
|
213622 |
28 |
0.35 |
0.2 |
500 |
0.1 |
0.35 |
0.2 |
0.04 |
0.2 |
|
|
|
213623 |
28 |
0.35 |
0.2 |
500 |
0.1 |
0.35 |
0.2 |
0.04 |
0.2 |
|
|
|
213624 |
28 |
0.35 |
0.2 |
500 |
0.1 |
0.35 |
0.2 |
0.04 |
0.2 |
|
|
|
213731 |
23 |
0.18 |
0.07 |
600 |
0.8 |
0.3 |
0.07 |
0.01 |
0.4 |
|
|
|
213760 |
23 |
0.18 |
0.07 |
600 |
0.8 |
0.24 |
0.07 |
0.01 |
0.4 |
|
|
|
213771 |
23 |
0.18 |
0.07 |
600 |
0.8 |
0.24 |
0.07 |
0.01 |
0.4 |
|
|
|
213800 |
86 |
3.8 |
1.1 |
55 |
2 |
1.5 |
0.2 |
0.2 |
0.6 |
|
|
|
213900 |
22 |
0.35 |
0.14 |
600 |
0.4 |
0.4 |
0.15 |
0.01 |
0.1 |
|
|
|
214120 |
86 |
3.8 |
1.1 |
50 |
1.4 |
1.5 |
0.2 |
0.2 |
0.6 |
|
|
|
214150 |
20 |
0.6 |
0.12 |
176 |
0.1 |
0.6 |
0.12 |
0.04 |
0.1 |
|
|
|
214160 |
20 |
0.55 |
0.13 |
176 |
0.1 |
0.55 |
0.13 |
0.04 |
0.6 |
|
|
|
216100 |
30 |
0.12 |
0.12 |
120 |
0.4 |
0.12 |
0.12 |
0.6 |
0.1 |
3 |
5 |
|
216200 |
22 |
0.2 |
0.12 |
140 |
0.2 |
0.31 |
0.12 |
0.6 |
0.1 |
3 |
5 |
|
216300 |
91 |
3.5 |
1.8 |
50 |
1.7 |
0.7 |
0.3 |
0.4 |
0.1 |
|
|
|
216400 |
22 |
0.25 |
0.12 |
140 |
0.2 |
0.31 |
0.12 |
0.6 |
0.1 |
3 |
5 |
|
216500 |
91 |
3.5 |
1.8 |
50 |
1.7 |
0.7 |
0.3 |
0.4 |
0.1 |
|
|
|
221100 |
65 |
0.77 |
0.07 |
85 |
1.2 |
0.18 |
0.02 |
0.3 |
0.1 |
100 |
30 |
|
221300 |
65 |
0.77 |
0.07 |
85 |
1.2 |
0.18 |
0.02 |
0.3 |
0.1 |
100 |
30 |
|
221500 |
65 |
0.77 |
0.07 |
85 |
1.2 |
0.18 |
0.02 |
0.3 |
0.1 |
50 |
10 |
|
221600 |
65 |
1.1 |
0.07 |
60 |
1.2 |
0.25 |
0.02 |
0.3 |
0.2 |
60 |
15 |
TS = Trockensubstanzanteil im Haupternteprodukt
NEP = N in der Frischsubstanz [kg/dt]
PEP = P in der Frischsubstanz [kg/dt]
ERT = maximale Erntemenge [kg/dt]
O = Anteil der oberirdischen Pflanzenteile im Verhältnis zum Haupternteprodukt
ON = N in der Frischsubstanz der oberirdischen Pflanzenteile [kg/dt]
OP = P in der Frischsubstanz der oberirdischen Pflanzenteile [kg/dt]
W = Anteil der Wurzeln im Verhältnis zum Haupternteprodukt
NW = N in der Frischsubstanz der Wurzeln [kg/dt]
WG = Jahre bis Wurzelreste im Gleichgewicht sind
OG = Jahre bis Speicher oberirdische Pflanzenreste im Gleichgewicht ist
Möglichkeiten der Beschreibung von Ernteentzug und Pflanzenrückführung
Inder Regel werden Kulturarten nicht als Gesamtpflanze geerntet, sondern es dem System werden bestimmte Pflanzeteile durch Ernteabfuhr entzogen. Generell ist es mit Wasmod möglich, zwischen Abfuhr, Rückfürung auf die Bodenoberfläche und Verbleib in der lebenden Pflanze zu unterscheiden. Damit ergeben sich für die Ernte bei Einbeziehung der 3 berücksichtigten Pflanzenfraktionen (s.o.) 8 Varianten (s. Tabelle).
|
Ernte-Code |
Pflanzenspeicher 1 Haupterntegut |
Pflanzenspeicher 2 oberirdische Pflanzenreste |
Pflanzenspeicher 3 Wurzeln |
|
81 |
Abfuhr |
Verbleib |
Verbleib |
|
82 |
Abfuhr |
Abfuhr |
Verbleib |
|
83 |
Abfuhr |
Abfuhr |
Abfuhr |
|
84 |
Rückführung |
Verbleib |
Verbleib |
|
85 |
Rückführung |
Rückführung |
Verbleib |
|
86 |
Rückführung |
Rückführung |
Rückführung |
|
87 |
Abfuhr |
Rüchführung |
Verbleib |
|
88 |
Abfuhr |
Rückführung |
Rückführung |
|
79 |
Milchviehbeweidung entkoppelt |
|
78 |
Weide mit 90% Nährstoffrückführung |
|
94 |
Leguminosen ohne Abfuhr |
|
95 |
Leguminosen, Abfuhr der Haupternteprodukte |
|
91 |
Weide mit 75% Nährstoffrückführung |
|
92 |
Weide mit 60% Nährstoffrückführung |
Pflanzenwachstum Buche
Damit der Kohlenstoff- und N-Haushalt von mehrjährigen Pflanzen angepaßt an das Pflanzenalter beschrieben werden kann, werden die Aufnahmekapazitäten getrennt für Blatt und nicht photosynthetisch aktive Pflanzenteile (z.B. der Buchenstamm) in Abhängigkeit vom Pflanzenalter dynamisiert.
- Blätter
0-20 Jahre : cblamax = 0.05x Jahr x 2750
> 20 Jahre : cblamax = 2750
mit: cblamax = maximale C-Aufnahmekapazität der Blätter
- Stamm
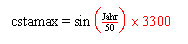
mit: cstamax = maximale C-Aufnahmekapazität des Stamms
In einer Testversion des Modells wurden weiterhin Abhängigkeiten dieser vegetationsspezifischen Größen zum Wasserhaushalt (Trockenstreß) und zum Stickstoffhaushalt eingeführt. Dabei konnte auf Zusammenhänge zurückgegriffen werden, die in dem Modell FAGUS (HOFFMANN 1995) beschrieben werden. Um diese komplexeren Abhängigkeiten zu integrieren, war es notwendig, Teilprozesse des pflanzlichen Kohlenstoffhaushalts einzubeziehen. In der aktuellen Version (4.0) wird vereinfachend die Vegetationsperiode von Laubbäumen in 2 Grobphasen unterteilt: Phase 1= Blattentwicklungsphase, Phase 2= Stammzuwachsphase. Phase 2 kann erst dann einsetzen, wenn Phase 1 einen Mindestwert an Kohlenstoffakkumulation erreicht hat. Der Anteil an Stickstoff, der in das Stammholz übergeht, hängt von der Menge an Kohlenstoff ab, die während der Phase 2 gebunden wird. Sowohl das Kohlenstoffbindungsvermögen als auch die Stickstoffbindung wird bei Wasser- bzw. N-Mangel eingeschränkt.
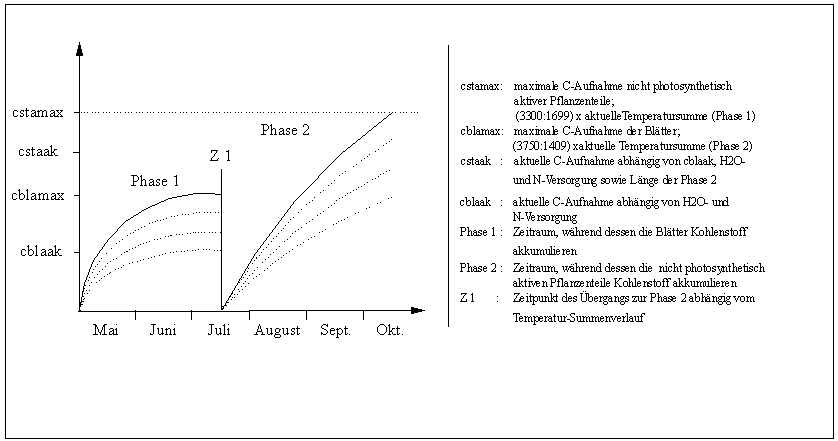
Abbildung 7 : Schematische Übersicht über die Partitionierung der Assimilation
N-Faktor
Der sog. N-Faktor bezieht die Reduktion der C-Aufnahme der Blätter bei N-Mangel in die Dynamisierung mit ein, wobei der aktuelle C-Gehalt (cblaa), ein spezifisches CN-Verhältnis als Grenzwert, oberhalb dessen N-Mangel angenommen wird (CNmin = 63) sowie die aktuelle N-Akkumulation in der Pflanzenmasse (pflme2) eine Rolle spielen. Wenn :
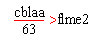
dann folgt für den aktuellen C-Gehalt der Blätter = pflme2 x CNmin
Datenverwaltung und -handhabung
Während die Handhabung von komplexen Modellen für Einzelberechnungen noch im interaktiven Betrieb (Parametereingabe am Bildschirm) vorstellbar ist, muß für die Bearbeitung größerer Gebiete, die aus einer Vielzahl von Einzelflächen bestehen, die Datenorganisation weitgehend automatisch ablaufen. Entscheidend ist hierbei, daß sich Parameterklassen entsprechend ihres räumlichen Bezuges definieren lassen. Während die Witterungs-Kenngrößen in der Regel für ein ganzes Gebiet (mehrere qkm) Gültigkeit haben, beziehen sich die Angaben zur Nutzung immer nur auf eine begrenzte Anzahl von Schlägen, auf denen die gleiche Fruchtfolge eingehalten wird und die in bezug auf Bearbeitungsmaßnahmen und Düngeraufwand vergleichbar sind. Die Parameter zur Beschreibung von Boden-, Relief- sowie Grund- und Oberflächenwasserverhältnissen gelten in der Regel nur für einen einzigen Flächenausschnitt. Die notwendigen statischen und dynamischen Eingabewerte werden aus vier Einzeldateien eingelesen.
Die Bodendatei beinhaltet die notwendigen bodenphysikalischen und -chemischen Kennwerte (Korngrößenverteilung, effektive Lagerungsdichte, Wassergehalt für unterschiedliche pF-Stufen, kf-Wert, pH-Wert, Anfangswassergehalt, Kompartimenttiefe) für alle vertikal angeordneten Kompartimente jeder Einzelfläche. Darüber hinaus werden hier weitere flächenbezogene Eingabeparameter zur Kennzeichnung der Flächengröße, des Oberflächen- und Grundwasserabflusses sowie der Nutzung und Fruchtfolge verwaltet.
Die Bodenstickstoffdatei enthält für jedes Kompartiment Anfangswerte für 3 Kohlenstoffpools (zugeführte organische Substanz, langfristig wenig mobiler Anteil und mikrobielle Biomasse), sowie Norg, Nitrat und Ammonium.
Die Klimadatei besteht aus tagesbezogenen Angaben zur Minimum- und Maximumtemperatur, zum Niederschlag, zum Sättigungsdefizit sowie zum atmosphärischen Stickstoffeintrag.
Die Nutzungsdatei beinhaltet jeweils für einzelne Kulturarten und Düngungsvarianten, entsprechend dem phänologischen Ablauf differenziert, Angaben zur Beschreibung der tiefenabhängigen Durchwurzelungsintensität, des pflanzentypischen Verdunstungsfaktors, des Blattflächenindex, der ausgebrachten Stickstoffmenge und -applikationsform sowie des durch die Ernte bedingten Stickstoffentzuges.
Für die Form der Ergebnisausgabe stehen je nach Fragestellung verschiedene Varianten zur Verfügung: Zustandsgrößen und Flußraten des Bodenwasserhaushalts (z. B. Bodenwasser- gehalte, Sickerraten, Transpirationsraten für einzelne Bodenkompartimente), des Bodenstickstoffhaushalts (Nitrat- und Ammoniumgehalt, Mineralisations- und Nitrifikationsraten) in Form von Zeitreihen, bezogen auf Einzelflächen sowie gebietsbezogene Bilanzgrößen (Grundwasserneubildung, Oberflächenabfluß, Stofffrachten in Grund- und Oberflächengewässer).
Um die Durchführung von gebietsbezogenen Modellrechnungen praktikabel zu gestalten, wurde das Modellsystem an ein Software-Umfeld angepaßt, durch welches zum einen die Bereitstellung der erforderlichen raumbezogenen Eingabeparameter erfolgt und wodurch zum anderen die Erstellung von Parameterdateien und die Auswertung von Ergebnisdateien weitgehend oberflächengesteuert und automatisiert abläuft. Durch die Anbindung an ein geographisches Informationssystem (GIS) werden auf der Grundlage der für die Modellrechnung relevanten Parameter zur Beschreibung der Bodeneigenschaften, der Reliefgestalt, der Vegetation und der anthropogenen Nutzung durch Verschneidung kleinste Geometrien, also Flächenausschnitte mit gleicher Ausstattung an für die Modellrechnung relevanten Kenngrößen, definiert. Diese Einzelflächen, deren Größe in Abhängigkeit von der Homogenität des Areals sehr unterschiedlich sein kann, stellen die räumliche Basis für Gebietssimulationsläufe dar und werden bei der Kennzeichnung der Modell-Eingabeparameter durch ihre Flächenschwerpunkte repräsentiert. Bei großer Variabilität von Hangneigung und Hangrichtung wird eine stark differenzierte Segmentierung in viele Einzelflächen erforderlich. Darüber hinaus liefert das GIS alle geometrischen Daten, die für die Modellrechnungen erforderlich sind: Flächengröße, Flächenumfang, inhaltliche Kennzeichnung und Koordinaten der punkt-, linien- und flächenhaften Elemente. Diese Daten werden wie in der Abbildung 4 dargestellt anhand eines Transformationsprogramms ("TOPTRA") ausgewertet. Dabei werden die folgenden für die Parameterfindung wichtigen Zuordnungs- und Ableitungsprozeduren durchgeführt:
- Bestimmung der Höhe über NN für einzelne Flächenschwerpunkte,
- Zuordnung der Höhe über NN für jeden Gewässerteilabschnitt,
- Abschätzung der mittleren Grundwassertiefe für jeden Flächenschwerpunkt unter Zugrundelegung des für die ungesättigte Zone abgeschätzten kf-Wertes, der mittleren Grundwasserneubildungsrate, des Gefälles zu jedem Vorfluterabschnitt sowie einer geschätzten Grundwasserzuflußrate,
- Zuordnung von Teilflächen und Vorfluterteilabschnitten entsprechend der Oberflächenabflußrichtung durch Ausweisung von Abflußkaskaden, die jeweils mit einer abflußlosen Mulde oder einem Vorfluterteilabschnitt abschließen. Dabei wird zusätzlich untersucht, ob die jeweilige Flächengrenze Oberflächenabfluß zuläßt oder als Abflußbarriere anzusehen ist.
Die für einen Modellauf notwendigen Eingabedaten zur Beschreibung des Witterungsverlaufes, zur Kennzeichnung phänologischer Charakteristika einzelner Kulturarten und zur Einbeziehung der landwirtschaftlichen Bearbeitungs- und Düngungsmaßnahmen werden in einer relationalen Datenbank verwaltet. Diese enthält auch die physikalischen und physikochemischen Bodenkennzahlen jeder Einzelfläche. Da in der Regel hierfür Meßergebnisse nicht flächenhaft vorliegen, wurden Programme implementiert, die die erforderlichen Werte von Kartierergebnissen (Bodenart und Bodentyp) ableiten. Häufig liegen lediglich die Profilbeschreibungen der Bodenschätzung vor. Aus diesem Grunde wurden Prozeduren entwickelt, welche diese Daten in die Sprache der wissenschaftlichen Bodenkunde umformen (BENNE et al. 1990).
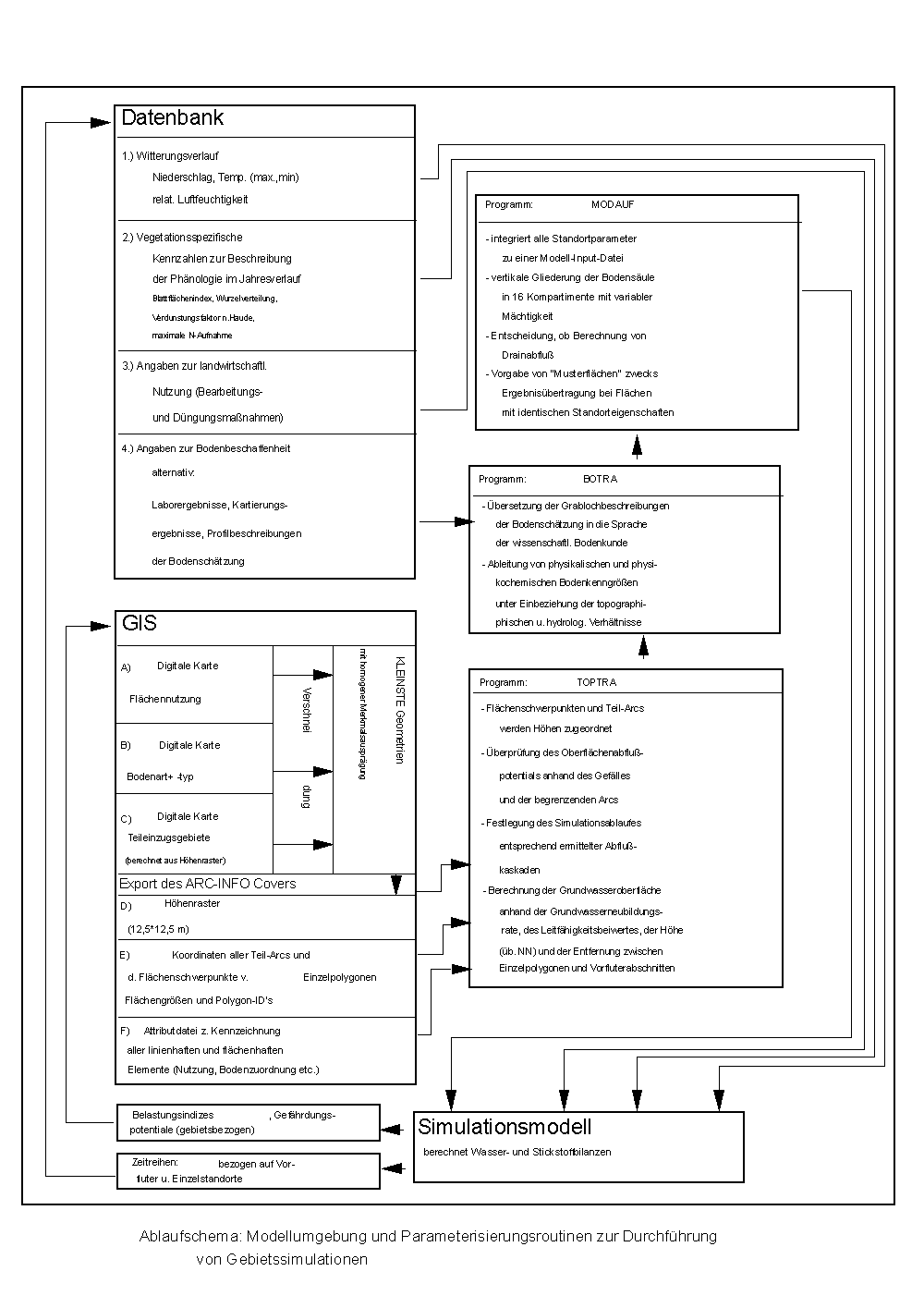
Abbildung 8 : Ablaufschema: Modellumgebung und Parametrisierungsprogramme zur Durch- führung von Gebietssimulationen
Informationen zum Umgang mit dem Modellsystem "WASMOD"
Formulierung von Zielsetzungen vor dem Modellansatz:
Bevor man mit dem von Parameterdateien beginnt, sollte man sich über die Formulierung von Fragestellungen, aufgrund derer man das Modell einsetzen will, im Klaren sein. Das Modell kann zusätzlich folgende Daten liefern:
1. Standortbezogene Wasserbilanzen (NDS, Interzeption, Evapotranspiration, Sickerwasseranteil, Dränabfluß, Grundwasserneubildungsrate)
2. Standortbezogene Zustandsgrößen zum Wasserhaushalt (Bodenwassergehalte, Saugspannungen, Grundwasserstände, Oberflächenwasserhöhe)
3. Standortbezogene Zustandsgrößen zum Bodenwärmehaushalt (Bodentemperaturen)
4. Standortbezogene Bilanzgrößen zum Kohlenstoffhaushalt: Nettoprimärproduktion (dynamisch nur bei der Buche, sonst aufbauend auf Tabellenfunktionen), Transformation der organischen Substanz im Boden (frische organische Substanz, mikrobielle Biomasse, langfristig stabileorganische Substanz), CO2-Freisetzung
5. Standortbezogene Zustandsgrößen des Kohlenstoffhaushaltes (Menge an leicht mineralisierbarer organischer Substanz, mikrobieller Biomasse, langfristig stabile organische Substanz in unterschiedlichen Bodenkompartimenten).
6. Standortbezogene Bilanzgrößen zum Stickstoffhaushalt (Mineralisations/Immobilisations-, Denitrifikations-, Nitrifikationsrate in unterschiedlichen Bodenkompartimenten), Nitratverlagerung, NO3- und NH4-Aufnahme durch die Pflanzenwurzel, Ammoniakverdampfung an der Bodenoberfläche, NH4- und Norg-Verlagerung von der Bodenoberfläche in den Oberboden, N-Rückführung durch Streu- und Pflanzenreste.
7. Standortbezogene Zustandsgrößen des Stickstoffhaushaltes ( Norg-, NH4- und NO3-Gehalte in unterschiedlichen Bodenkompartimenten, NO3-Konzentration im Grundwasser, N-Gehalte in der Pflanze).
Zeitschrittwahl
Das Modellsystem besteht aus verschiedenen Teilmodellen, die mit teilweise unterschiedlichen Zeitschritten arbeiten. Für die Berechnung der vertikalen Wasser- und Stoffbewegung ist die Zeitschrittanzahl flexibel, angepaßt an die berechnete Sickerwassermenge (6 - 200 Schritte pro Tag). Das Bodentemperatur-Teilmodell rechnet in 6 Zeitschritten pro Tag; die Berechnung der mikrobiell gesteuerten Prozesse des Stickstoffhaushaltes erfolgt einmal täglich. Prinzipiell ist es nicht sinnvoll Modellresultate in einer kleineren zeitlichen Auflösung als Tageswerte auszugeben, da auch die klimatischen Input-Daten nicht feiner aufgelöst sind. Zur Zeit kann die Ausgabe in täglicher, wöchentlicher oder jährlicher Auflösung erfolgen.
Beschaffung der Eingangsdaten
Für die Anwendung des Modellsystems WASMOD ist die Vorgabe einer größeren Anzahl von boden-, relief- und nutzungsspezifischen Eingabeparametern notwendig, die in Regel vor Ort zu erheben sind. Um die Möglichkeit der Modellanwendung auch für solche Standorte anzubieten, für die die umfangreichen Datenerhebungen nicht durchgeführt worden sind, sind eine Reihe von Ableitungs- und Aggregierungsprogrammen entwickelt worden. Dadurch ist es möglich, auf der Basis von Daten der Bodenschätzung, der Deutschen Grundkarte 1/5000, sowie der Gemeinde- und Agrastatistik Simulationsläufe für größere Gebiete durchzuführen. Die Kalibrierung dieser Programme wurde bisher für Gebiete des Bundeslandes Schleswig-Holstein durchgeführt (siehe nn).
Beschreibung der Eingabedaten
Die Inputdaten ließt das Modellprogramm aus 4 Einzeldateien ein, wobei die Erstellung dieser Parameterdateien in automatisierter Form geschieht:
|
Bodendatei : |
beinhaltet alle bodenphysikalischen und bodenchemischen Kennwerte für unterschiedliche vertikal angeordnete Kompartimente sowie standortabhängige Angaben wie Flächengröße, Nutzungsvariante, Abstand zum Vorfluter, Hangneigung etc. |
|
Bodenstickstoff- und Kohlenstoffdatei: |
enthält für jedes Bodenkompartiment Anfangswerte für unterschiedliche N-Formen
1. AOM (zugeführte organ. Substanz 1 und 2)
2. BOM (organ. Subst. in Biomassen ; 1 und 2)
3. SOM (dauerhaft kaum mineralisierbarer Anteil d. org. Subst; 1 u. 2)
4. Norg (organisch gebundener Stickstoff)
5. NH4 (Ammonium)
6. NO3 (Nitrat) |
|
Klimadatei : |
enthält auf Tagesbasis Meßwerte für Niederschlag, Maximum-Temperatur, Minimum-Temperatur, Sättigungsdefizit und die als atmosphärische Deposition eingetragene N-Menge |
|
Nutzungsdatei : |
enthält Daten zur Beschreibung der tiefenabhängigen Durchwurzelungsintensität, des pflanzentypischen Verdunstungsfaktors, des Blattflächenindex, der N-Düngermenge, Düngervariante, N-Entzug durch Ernte und Bearbeitungsmaßnahmen |
Boden- und standortbezogene Eingabeparameter
Routinemäßig wird zur Zeit mit 15 vertikal angeordneten Kompartimenten gerechnet, wobei die Kompartimentmächtigkeit von oben nach unten zunehmen sollte. Es hat sich als vorteilhaft herausgestellt, Kompartiment 1 und 2 mit einer Mächtigkeit von 5 cm festzulegen, den folgenden 9 Kompartimenten (3-11) sollte eine vertikale Ausdehnung von 10 cm zugeordnet werden, die dann folgenden Kompartimente sind entsprechend des Grundwasserabstandes festzulegen. Die in Tabelle 3 aufgeführten Parameter sind für jedes einzelne Kompartiment anzugeben.
Tabelle 3 : Bodenphysikalische Kenngrößen (für einzelne Kompartimente anzugeben)
|
Bezeichnung |
Einheit |
Erläuterungen |
|
Kompartimentnummer |
|
durchlaufende Numerierung der Bodenkompartimente (1 - 15) |
|
Kompartimenttiefe |
cm |
vertikaler Durchmesser der Einzelkompartimente |
|
Gehalt an org. Koh-lenstoff |
% d. TS |
Meßwerte oder aus Bodenansprache abgeleitete Werte |
|
Ton-Gehalt (< 2 ) |
% d. TS |
Meßwerte o. a. Bodenansprache abgeleitete Werte |
|
Schluffgehalt (< 63 ) |
% d. TS |
Meßwerte o. a. Bodenansprache abgeleitete Werte |
|
Effektive Lagerungsdichte |
cm3 |
Stechzylindermessungen oder aus Bodenansprache abgeleitete Werte |
|
kf-Wert |
cm pro Tag |
Labormessungen o. a. Bodenansprache abgeleitete Werte |
|
Wassergehalt für die PF-Stufen 0, 1.8, 2.5, 3.5 und 4.2 |
Vol.% |
Labormessungen oder aus Bodenansprache abgeleitete Werte |
|
pH-Werte |
|
Labormessungen oder Schätzwerte |
|
Anfangsbodenfeuchten |
Vol.% |
Gravimetrie-Meßergebnisse, Schätzwerte (z.B. Feldkapazität) |
Die letzten beiden Spalten beinhalten standortbezogene Angaben zur Kennzeichnung der Vegetation bzw. Fruchtfolge sowie geometrische Kennwerte zur Charakterisierung der Grundwasser-, Oberflächenwasser- und Dränwasserabflußsituation (siehe Tabelle 4).
Tabelle 4 : Angaben zur topographischen Situation und zur Landnutzung
|
Polygonnummer |
Codenummer |
ermöglicht den Bezug zu Einzelflächen der in ARC/INFO digital verwalteten Karten |
|
Flächengröße |
ms |
wird aus einer ARC/INFO-Datei übernommen |
|
Höhe ü.N.N.d. Fl.schw.pkt. |
in m |
wird über vorhande Informationen zum Relief u. Gewässernetz ermittelt |
|
Nutzung und Fruchtfolge |
Codenummer |
wird ermittelt durch Kartierung, Luftbildauswertung u. Befragung |
|
Vorfluter f. Grund- wasserabfluß |
Codenummer |
wird über vorhandene Informationen zum Gewässernetz und zur Wasserleitfähigkeit abgeleitet |
|
Entfernung zum Vorfluter (GA) |
in m vom Flächenschw.pkt |
wird über vorhandene Informationen zum Relief u. Gewässernetz ermittelt |
|
Höhe ü.N.N.d. Vorfluter (GA) |
in m |
wird über vorhandene Informationen zum Relief u. Gewässernetz ermittelt |
|
Höhe ü.N.N.d. Vorfluter (OA) |
in m |
wird über vorhandene Informationen zum Relief u. Gewässernetz ermittelt |
|
ZugeordneteNachbarfläche |
Codenummer |
bezeichnet die Nachbarfläche in die Oberflächenabfluß gelangt |
|
Länge der Ob.-Abflußstrecke |
in m |
Bezug: entweder Schwerpunkt der Nachbarfläche oder zugeordneter Vorfluter |
|
Vorfluter für Ober-flächenabfluß |
Codenummer |
wird über vorhandene Informationen zum Relief und zum Gewässernetz ermittelt |
|
Entfernung z. Vorfluter (OA) |
in m vom Flächenschwpkt.* |
wird über vorhandene Informationen zum Relief u. Gewässernetz ermittelt |
|
Gefälle für Oberfl.Abfluß |
in % |
Bezug: entweder Schwerpunkt der Nachbarfläche oder zugeordneter Vorfluter |
|
Abflußbarriere |
ja = 1 nein = 0 |
ja, wenn der Oberflächenabfluß durch ein linienhaftes Element unterbrochen wird |
|
Drän-Tiefe |
in cm |
Angabe nur, wenn Dränabfl. berechnet werden soll |
|
Drän-Abstand |
in cm |
Angabe nur, wenn Dränabfl. berechnet werden soll |
|
Drän-Durchmesser |
in cm |
Angabe nur, wenn Dränabfl. berechnet werden soll |
* GA = Grundwasserabfluß OA = Oberflächenabfluß Schwpkt. = Flächenschwerpunkt
Die Klimadaten und optional auch Angaben zum Depositionseintrag werden in der Szenariodatei verwaltet. Das Modell erfordert einen Minimaldatensatz, der die durch einfache Klimameßstationen erfaßbaren Parameter (Niederschlag, Lufttemperaturmin,max sowie das Wassersättigungsdefizit der bodennahen Luftschicht) beinhaltet.
Die Szenariodatei umfaßt folgende Variable:
_________________________________________________________________________
Nummer des Tages : vom 1- 365 (366)
Wochennummer : ermöglicht den Bezug zur Nutzungsdatei
Tagesniederschlagssumme : in mm
Maximum-Lufttemperatur : °C
Minimum-Lufttemperatur : °C
Sättigungsdefizit : 14 Uhr (mm Hg)
Stoffeintrag : Tagessumme der Gesamtdeposition eines Stoffes (g/ms)
___________________________________________________________________________
Die Umrechnung von Meßwerten der relativen Luftfeuchte zum Sättigungsdefizit kann durch Anwendung eines einfachen FORTRAN/dBASE-Programmes (Name?) durchgeführt werden. In Tabelle 5 ist ein Beispiel einer Klimadatei dargestellt.
Tabelle 5 : Beispiel Klimadatei
|
Satz# |
XTAG |
T2 |
NDS |
N2 |
N3 |
TEMP1 |
TEMP2 |
HUM |
|
1 |
274 |
19 |
4.90 |
1 |
0 |
12.40 |
7.45 |
3.55 |
|
2 |
275 |
19 |
10.40 |
1 |
0 |
13.60 |
7.90 |
6.48 |
|
3 |
276 |
19 |
0.00 |
1 |
0 |
15.20 |
5.16 |
5.02 |
|
4 |
277 |
19 |
0.50 |
1 |
0 |
15.79 |
9.56 |
8.72 |
|
5 |
278 |
19 |
0.00 |
1 |
0 |
16.24 |
8.47 |
3.65 |
|
6 |
279 |
19 |
0.00 |
1 |
0 |
13.99 |
8.13 |
2.49 |
|
7 |
280 |
19 |
0.00 |
1 |
0 |
14.36 |
7.62 |
2.55 |
|
8 |
281 |
19 |
0.00 |
1 |
0 |
17.89 |
10.67 |
4.87 |
|
9 |
282 |
19 |
0.10 |
1 |
0 |
18.74 |
11.47 |
6.70 |
|
10 |
283 |
19 |
0.10 |
1 |
0 |
18.93 |
9.74 |
5.51 |
xtag= Tag im Jahr,
T2 = Zuordnung phänologische Phase (14 tägiger Wechsel im mittleren Verlauf)
NDS= Niederschlag in mm
N2, N3 = nicht belegt
Temp1 = Temperatur-Tagesmaximum
Temp2 = Temperatur Tagesminimum
Hum = Luftfeuchtigkeit (14 Uhr)
Tabelle 6 : Beispiel Bodenparameter-Datei
Tabelle 7 : Beispiel C/N-Parameter-Datei
|
Satz# |
HORI |
AOM1 |
AOM2 |
BOM1 |
BOM2 |
SOM0 |
SOM1 |
SOM2 |
Norg |
NH4 |
NO3 |
|
1 |
1 |
60.5 |
0.0 |
23.4 |
21.4 |
0.0 |
9484.4 |
3406.4 |
1376.7 |
1.00 |
0.84 |
|
2 |
2 |
60.5 |
0.0 |
23.4 |
21.4 |
0.0 |
9484.4 |
3406.3 |
1376.7 |
0.98 |
0.68 |
|
3 |
3 |
120.9 |
0.0 |
46.7 |
42.8 |
0.0 |
18968.8 |
6812.7 |
2753.5 |
1.61 |
1.82 |
|
4 |
4 |
120.9 |
0.0 |
46.7 |
42.8 |
0.0 |
18968.8 |
6812.6 |
2753.5 |
1.67 |
1.90 |
|
5 |
5 |
0.0 |
0.0 |
1.5 |
3.0 |
0.0 |
6936.3 |
830.8 |
699.0 |
1.00 |
0.66 |
|
6 |
6 |
0.0 |
0.0 |
0.7 |
1.4 |
0.0 |
3288.6 |
382.5 |
330.5 |
0.65 |
0.51 |
|
7 |
7 |
0.0 |
0.0 |
0.7 |
1.4 |
0.0 |
3287.1 |
361.4 |
328.3 |
1.00 |
0.45 |
|
8 |
8 |
0.0 |
0.0 |
0.7 |
1.4 |
0.0 |
3287.1 |
360.1 |
328.0 |
1.00 |
0.81 |
|
9 |
9 |
0.0 |
0.0 |
0.7 |
1.4 |
0.0 |
3287.1 |
361.2 |
328.4 |
1.00 |
0.57 |
|
10 |
10 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
1.2 |
0.0 |
0.50 |
1.25 |
|
11 |
11 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.6 |
0.0 |
0.50 |
0.60 |
|
12 |
12 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
1.1 |
0.0 |
0.50 |
3.70 |
|
13 |
13 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
1.5 |
0.0 |
0.50 |
5.02 |
|
14 |
14 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
6.2 |
0.0 |
0.50 |
56.52 |
|
15 |
15 |
0.0 |
0.0 |
0.0 |
0.1 |
0.0 |
3.7 |
32.1 |
0.0 |
0.50 |
392.33 |
AOM= zugef. organ. Substanz 1, OP2= zugeführte organ. Substanz 2,
BOM= organ. Substanz in Biomasse (1. u. 2)
, SOM= dauerhaft kaum mineralisierbarer Anteil der organischen Substanz
1 = langfristig mineralisierbarer Anteil
, 2 = schnell mineralisierbarer Anteil
Norg= organische gebundener Stickstoff
, NH4=Ammonium, NO3= Nitrat
Die Kennzeichnung der Phänologie unterschiedlicher Pflanzenbestände erfolgt im wesentlichen über drei Parameter (vgl. Tabelle 8):
- Durchwurzelungstiefe (Tiefe unter der Bodenoberfläche bis zu der der Hauptwurzelanteil reicht). Dieser Wert bestimmt aus welchem/n Bodenkompartiment(en) der Wasserentzug entsprechend der Transpirationsrate sowie die Stickstoffaufnahme erfolgen. Bei einer angegebenen Wurzeltiefe von <= 5cm findet keine Stickstoffaufnahme statt (z.B. Angabe bei Vegetationsruhe in Wintermonaten).
- Der HAUDE-Faktor wird benötigt, um auf der Grundlage des Sättigungsdefizits der bodennahen Luftschicht eine vegetationsspezifische potentielle Evapotranspirationsrate abzuschätzen.
- Die Angaben zum Blattflächenindex (LAI) bestimmen die Berechnung des Interzeptionsverlustes und dienen als Hilfsgröße bei der Abschätzung des Energieeintrages durch direkte Strahlung im Rahmen der Bodentemperaturmodellierung.
Tabelle 8 : Pflanzenabhängige Kenngrößen und landwirtschaftliche Bearbeitungsmaßnahmen
|
Bezeichnung |
Einheit |
Erläuterungen |
|
Durchwurzelungstiefe |
cm unter Flur |
zur Berechnung der relativen Wurzelverteilung |
|
HAUDE-Faktoren k |
|
zur Berechnung der pot. Evapotranspiration |
|
Blattflächenindex |
cm2/cm2 |
zur Berechnung des Interzeptionsverlustes |
|
Nährstoff-Eintrag durch Düngung |
in kg/ha |
ermittelt durch eine Fragebogenerhebung oder Gemeindestatistik |
|
Düngerart |
org. N
NH4, NO3 |
ermittelt durch eine Fragebogenerhebung oder Gemeindestatistik |
|
Bearbeitungsmaßnahme |
Kennziffer
z.B.:Ernte |
ermittelt durch eine Fragebogenerhebung od. Gemeindestatistik |
Die Angaben zur Charakterisierung der Durchwurzelungstiefe, der Blattfläche und der vegetationsspezifischen Transpiration (HAUDE-Faktor) gelten jeweils für einen Zeitraum von 14 Tagen
Die genannten Angaben zum Phänologieverlauf können sowohl zur Kennzeichnung eines spezifischen Jahresganges in das Modell eingehen, als auch als Standarddatensatz zur Kennzeichnung des über viele Jahre gemittelten Ablaufes Verwendung finden. Im zweiten Fall erfolgt eine an den Temperaturverlauf spezifischer Jahre angepaßte Phänologiekorrektur im Rahmen der Simulationsrechnung statt. Dabei wird der aktuelle Temperatursummenverlauf mit einem über 30 Jahre gemittelten Temperatursummenverlauf verglichen, auftretende Differenzen führen zu einer beschleunigten bzw. verzögerten Phänologieentwicklung. Wichtig ist es, darauf hizuweisen, daß diese Tabellenfunktionen zur Kennzeichnung der mittleren Temperatursummen standortabhängig ist und sich in der Standardmodellversion auf schleswig-holsteinische Verhältnisse bezieht
Tabelle 9 : Beispiel einer Phaeno-Datei
|
Wurzeltiefe |
Haude- faktor |
LAI |
N-Eintr. d. Düng. |
Bearbeit. Maßnahme |
Zetliche Verschieb. v. Bezugsdatum |
|
5.00 |
0.15 |
0.00 |
22.00 |
99.00 |
0 |
|
5.00 |
0.15 |
0.00 |
0.00 |
0.00 |
0 |
|
5.00 |
0.15 |
0.00 |
0.00 |
0.00 |
0 |
|
5.00 |
0.15 |
0.00 |
0.00 |
0.00 |
0 |
|
5.00 |
0.15 |
0.00 |
0.00 |
0.00 |
0 |
|
5.00 |
0.15 |
0.00 |
13.50 |
14.00 |
1 |
|
5.00 |
0.22 |
1.00 |
0.00 |
0.00 |
0 |
|
15.00 |
0.27 |
1.00 |
0.00 |
0.00 |
0 |
|
40.00 |
0.32 |
1.20 |
1.50 |
21.00 |
0 |
|
50.00 |
0.38 |
1.50 |
0.00 |
0.00 |
0 |
|
50.00 |
0.42 |
2.00 |
0.00 |
0.00 |
0 |
|
50.00 |
0.44 |
2.00 |
0.00 |
0.00 |
0 |
|
50.00 |
0.46 |
2.00 |
0.00 |
0.00 |
0 |
|
50.00 |
0.42 |
2.00 |
0.00 |
0.00 |
0 |
|
50.00 |
0.35 |
1.50 |
0.00 |
0.00 |
0 |
|
5.00 |
0.20 |
0.00 |
12.07 |
19.00 |
1 |
|
5.00 |
0.20 |
0.00 |
0.00 |
0.00 |
0 |
|
5.00 |
0.15 |
0.00 |
0.00 |
0.00 |
0 |
|
30.00 |
0.20 |
0.00 |
0.00 |
0.00 |
0 |
|
30.00 |
0.20 |
0.00 |
0.00 |
0.00 |
0 |
|
30.00 |
0.20 |
0.00 |
0.00 |
0.00 |
0 |
|
30.00 |
0.20 |
0.00 |
0.00 |
0.00 |
0 |
|
30.00 |
0.20 |
0.00 |
0.00 |
0.00 |
0 |
|
30.00 |
0.20 |
0.00 |
0.00 |
19.00 |
10 |
Quelle: REICHE, E.-W., 1990: Entwicklung, Validierung und Anwendung eines Modellsystems zur Beschreibung und flächenhaften Bilanzierung der Wasser- und Stickstoffdynamik in Böden. Kiel.
Weiterhin werden in den Phänodateien Angaben zum Nährstoffeintrag durch Düngung, zur pflanzenspezifischen Aufnahmekapazität und zu einzelnen landwirtschaftlichen Bearbeitungsmaßnahmen gemacht:
- Nährstoffeintrag durch Düngung. Es werden die Mengenangaben für einzelne Düngertermine geliefert. Diese Mengen beziehen sich auf Varianten, die in der folgenden Spalte (in der Nährstoffart) spezifiziert werden (siehe Tabelle 9). Der Aussaattermin wird hier mit der Kennummer 99 bezeichnet. In die Spalte Nährstoffmenge ist hier die Aufnahmekapazität, bezogen auf die gesamte Vegetationsperiode, anzugeben (z.B. bei Weizen 220 kg N). Der Erntetermin wird in der Spalte Nährstoffart durch die Ziffer 19 gekennzeichnet. Es kann sowohl mit einer fest vorgegebenen Erntemenge, als auch mit einer modellhaft ermittelten gerechnet werden. Die Abschätzung der Nährstoffrückführung durch Erntereste erfolgt kulturartspezifisch auf der Grundlage von Literaturangaben.
Tabelle 10 : Kennziffern zur Nährstoffart
|
Codenummer |
Nährstoffart |
|
99,00 |
Aussaat, Aufnahmekapazität |
|
19,00 |
Ernte |
|
11,00 |
Schweinegülle |
|
12,00 |
Rindergülle |
|
13,00 |
Mischgülle |
|
14,00 |
Mist mit Einarbeitung in die ersten 30cm des Bodens |
|
15,00 |
Mist mit Einarbeitung in die ersten 5cm des Bodens |
|
21,00 |
Ammonsalpeter mit Ammoniumeinarbeitung ins oberste Boden-Kompartiment (50 % NO3, 50 % NH4) |
|
22,00 |
reiner Ammoniumdünger u. Einarbeitung i. oberste Boden-K. |
|
23,00 |
Ammonsalpeter ohne Einarbeitung |
|
24,00 |
noch nicht |
|
25,00 |
noch nicht |
Modell-Output
Die Modellresultate lassen sich grundsätzlich in Zustandsgrößen und Raten gliedern. Zur Zeit liegen eine Reihe von Ausgabemodi vor, die sich vor allem in ihrer zeitlichen Auflösung unterscheiden (Tag, Woche, Jahr). Die Auswahl an Ausgabevariablen hängt von der jeweiligen zu bearbeitenden Fragestellung ab, so daß eine Erweiterung dieser Variablenliste ohne weiteres durchführbar ist. Unabhängig von dem jeweils gewählten Ausgabemodus werden Abschlußbilanzen erstellt. Handelt es sich um einen Simulationslauf, der sich nur auf einen Standort bezieht, so können die Abschlußbilanzen mehrerer Jahre in die gleiche Datei geschrieben werden. Bei Gebietssimulationen werden die Bilanzen für jedes Einzelpolygon nacheinander in den Dateien "Bilanw" und "Bilans" abgelegt. Diese beinhalten für den Wasserhaushalt folgende Informationen :
Bilanw: Abschluß-Bilanz-Wasser (in cm Wasser)
Cudb1: Polygonnummer
Cudb2: Fläche in ms
Cudb4: Nutzungsnummer laut Nutzungsschlüssel (im Bezugsjahr)
Sumnds: Niederschlagssumme (in cm)
Sumvin: Interzeption (Summe; in cm)
Sumeta akt. Evapotranspiration (Summe; in cm)
Grust: Grundwasserstand (letzter Simulationsschritt; in cm unter Flur)
Delges : Bodenwassergehalts-Veränderung i.d. Simulationsperiode (in cm)*
Delta(KZA): Sickerwassermenge (Summe; in cm)*
Ofla: Oberflächenwasser gestaut (Endzustand; in cm)
Sumab: Grundwasserabfluß (in cm)
Draisu: Dränwasserabfluß (in cm)
Sumfla: Oberflächenwasserabfluß (in cm)
Sumopo: Oberflächenwassereintrag durch benachb. Fläche (in cm)
* bezieht alle Kompartimente mit ein, die oberhalb der angegebenen Bilanzierungstiefe liegen (siehe Modellaufruf)
Tabelle 11 : Beispiel einer Bilanw-Datei
|
1320.0 |
1598.96 |
213213.0 |
73.40 |
18.6 |
21.1 |
604.9 |
-0.3 |
-33.9 |
0.0 |
27.0 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
69.54 |
16.8 |
27.5 |
605.6 |
-0.1 |
-25.3 |
0.0 |
16.9 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
59.45 |
16.7 |
30.2 |
606.4 |
0.2 |
-12.3 |
0.0 |
27.7 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
88.04 |
18.3 |
27.3 |
604.8 |
0.8 |
-41.7 |
0.0 |
18.8 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
85.38 |
19.8 |
29.5 |
606.1 |
1.3 |
-34.9 |
0.0 |
45.9 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
82.29 |
18.1 |
30.8 |
606.3 |
-1.0 |
-34.4 |
0.0 |
41.4 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
75.92 |
18.4 |
29.5 |
605.6 |
-0.5 |
-28.6 |
0.0 |
24.9 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
69.96 |
13.6 |
31.0 |
604.8 |
-1.6 |
-26.8 |
0.0 |
35.0 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
88.82 |
18.4 |
30.3 |
604.0 |
1.2 |
-38.9 |
0.0 |
22.1 |
0.0 |
0.0 |
0.0 |
0 |
|
1320.0 |
1598.96 |
213213.0 |
54.20 |
14.4 |
30.4 |
607.0 |
1.4 |
-7.9 |
0.0 |
27.7 |
0.0 |
0.0 |
0.0 |
0 |
Wird die Stickstoffdynamik in die Simulationsrechnung einbezogen (Angabe bei Programmstart 1= volle Stickstoffsimulation), so umfaßt die Stickstoffabschlußbilanz folgende Variablen:
Bilans: (Abschluß-Bilanz-Stickstoff, in kg N/ha)
Cudb1 Polygonnummer
sumein N-Eintrag (in kg/ha)
sxme NO3+NH4-Menge zum Simulationsende (in kg N/ha)
xgkonz Grundwasserkonzentration (mg NO3-N/l)
smegru Menge im Grundwasser absolut (in kg N/ha)
deme11 Sickerverlust (aus 100 cm Tiefe; in kg N/ha)
pflme Gesamternteentzug (in kg N/ha)
pflme2 Ernteentzug durch die letzte Ernte (in kg N/ha)
DSMIN Gesamt-Mineralisationsrate (in kg N/ha)
UPNH4 Gesamt-Ammonium-Aufnahme (in kg N/ha)
Nitrif Gesamt-Nitrifikationsrate (in kg N/ha)
SRDNIT Gesamt-Denitrifikationsrate (in kg N/ha)
SVOL Gesamt-NH4-Verluste an d. Atmosph. (in kg N/ha)
xmedsu Desamt-N-Verluste in Dränage (in kg N/ha)
Denitr2 Denitrifikation bis zum n-ten Kompartiment (n wird im der com.-dt. angegeb.)
N-Rueck N-Rueckführung durch Pflanzenreste
pnbis N-Bilanz Pflanze
bnbis N-Bilanz-Boden
norgein N-org Eintrag als Teilmenge des Gesamteintrags (nur externe Einträge)
xeins1j Austrag über Interflow
Tabelle 12 : Beispiel einer Bilans-Datei
|
28.0 |
10105.0 |
13.6 |
8.4 |
0.1 |
41.2 |
-22.8 |
10.4 |
59.6 |
82.4 |
45.5 |
45.8 |
2294.5 |
2750.0 |
2825.3 |
|
28.0 |
10105.0 |
13.6 |
6.0 |
0.1 |
32.2 |
-9.9 |
12.8 |
52.2 |
60.3 |
41.1 |
30.8 |
2825.4 |
2750.0 |
2478.4 |
|
28.0 |
10105.0 |
13.6 |
5.3 |
0.1 |
24.5 |
-7.0 |
13.5 |
54.6 |
60.0 |
43.5 |
31.2 |
2974.6 |
2750.0 |
2497.8 |
|
28.0 |
10105.0 |
13.6 |
4.4 |
0.1 |
20.7 |
-17.9 |
11.5 |
58.6 |
75.0 |
47.7 |
40.6 |
2538.5 |
2750.0 |
2691.0 |
|
28.0 |
10105.0 |
13.6 |
8.4 |
0.1 |
34.2 |
-14.1 |
13.6 |
57.6 |
77.3 |
49.9 |
40.6 |
2982.7 |
2750.0 |
2816.9 |
|
28.0 |
10105.0 |
13.6 |
7.6 |
0.1 |
30.1 |
-20.1 |
14.9 |
56.6 |
79.0 |
49.9 |
41.0 |
3267.3 |
2750.0 |
2774.2 |
|
28.0 |
10105.0 |
13.6 |
7.6 |
0.1 |
20.2 |
-14.4 |
14.3 |
51.3 |
68.9 |
44.6 |
35.2 |
3137.9 |
2750.0 |
2576.9 |
|
28.0 |
10105.0 |
13.6 |
0.9 |
0.1 |
23.3 |
-20.9 |
12.6 |
40.5 |
49.9 |
40.1 |
27.9 |
2774.8 |
2750.0 |
1926.7 |
|
28.0 |
10105.0 |
13.6 |
4.4 |
0.1 |
17.8 |
-8.9 |
11.0 |
44.8 |
58.5 |
45.1 |
25.0 |
2417.9 |
2750.0 |
2974.4 |
|
28.0 |
10105.0 |
13.6 |
9.2 |
0.1 |
18.8 |
-2.3 |
13.3 |
55.1 |
63.6 |
41.5 |
34.9 |
2936.0 |
2750.0 |
2588.9 |
Um die wesentlichen Zustandsgrößen und Flußraten in Form von Wochenwerten zu erhalten, muß die Ausgabenummer 22 gewählt werden. Bezogen auf den Wasserhaushalt finden sich folgende Angaben in der Datei "Result":
Bilanc: gibt Poolgrößen des Kohlenstoff-, Stickstoff und Wasserhaushalts jeweils bezogen auf den Anfangs- und Endtermin eines Simulationszeitraumes an.
Tabelle 12a: Beispiel einer Bilanc-Datei
|
Polynummer |
Fläche in Hektar |
xxx |
C-Boden Anfangsgehalt |
C-Boden Endgehalt |
N-Boden Anfangsgehalt |
N-Boden Endgehalt |
Wasser-Boden Anfangsgehalt |
Wasser-Boden Endgehalt |
N-Pflanze Anfangsgehalt |
N-Pflanze Endgehalt |
C-Pflanze Endgehalt (mehrjährige Pflanzen) |
|
28.000 |
20000.000 |
322200.000 |
99952.6 |
99889.9 |
10463.0 |
10281.0 |
1483.0 |
1498.8 |
0.0 |
0.5 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
99890.1 |
100049.6 |
10280.9 |
10217.3 |
1498.8 |
1778.0 |
0.0 |
0.6 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
100049.6 |
99629.0 |
10217.4 |
10154.0 |
1778.0 |
1628.9 |
0.0 |
0.7 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
99629.4 |
100219.7 |
10154.0 |
10063.4 |
1629.0 |
1526.8 |
0.0 |
0.1 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
100222.6 |
100672.2 |
10078.7 |
10086.5 |
2247.3 |
2205.1 |
0.0 |
0.4 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
100671.9 |
98950.6 |
10086.6 |
9929.8 |
2205.3 |
2273.3 |
0.0 |
11.4 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
98950.4 |
99585.9 |
9929.7 |
9873.7 |
2273.1 |
2195.4 |
0.0 |
2.3 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
99586.1 |
98743.1 |
9873.7 |
9793.1 |
2195.6 |
2160.0 |
0.0 |
42.8 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
98743.2 |
100059.7 |
9793.0 |
9711.7 |
2159.9 |
2350.3 |
0.0 |
0.1 |
0.0 |
|
28.000 |
20000.000 |
322200.000 |
100059.4 |
97412.6 |
9711.7 |
9615.7 |
2350.3 |
2513.2 |
0.0 |
30.0 |
2909.6 |